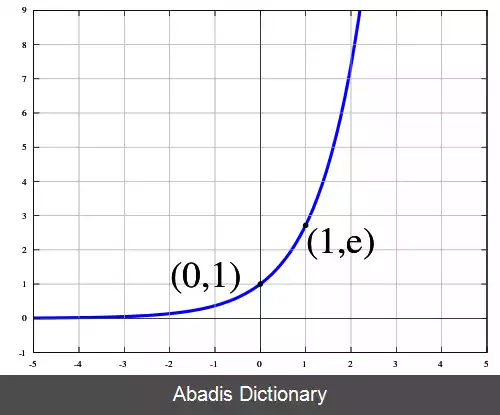
تابع نِمایی[ ۱] یا نموی ( به انگلیسی: Exponential function ) تابعی مهم در ریاضیات است و معمولاً به صورت exp ( x ) یا e x نوشته می شود که e عدد اویلر ( ثابت نپر ) با مقدارِ تقریبی ۲٫۷۱۸۲۸۱۸۲۸ است.
در واقع، تابع لگاریتم عکس تابع نمایی است.
البته، این تابع را می توان به صورت a x نیز تعریف کرد. استفاده از لگاریتم نشان می دهد که:
این تابع را تابع نمایی با پایهٔ a می خوانیم که a عددی ثابت است.
در بسیاری از علوم وقتی از تابع نمایی صحبت می شود، منظور تابع k a x است.
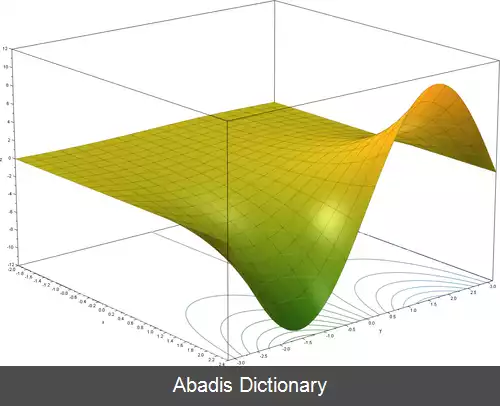
عموماً متغیر x می تواند هر عدد حقیقی یا مختلط باشد. به عبارت دیگر، معکوس ln ( y ) = x را exp ( x ) = e x = y گویند.
تابع a − x قرینه تابع a x می باشد.
y = a − x = ( 1 a ) x
نکته: این دو تابع نسبت به محور yها قرینه یکدیگر هستند.
تابع − a x قرینه تابع a x می باشد.
نکته: این دو تابع نسبت به محور Xها قرینه یکدیگر هستند.
• تابع نمایی معکوسِ تابع لگاریتم طبیعی ( Y=ln ( x است.
• دامنه آن تمام اعداد حقیقی است.
• برد آن تمام اعداد مثبت است.
• مشتق آن همواره با خودش برابر یا بزرگ تر و تابعی پیوسته و صعودی از x است.
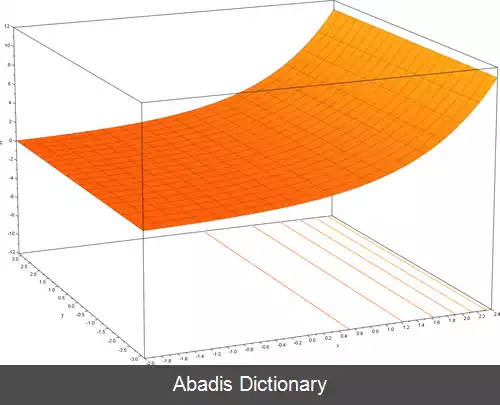
نمودار تابع نمایی دو حالت کلّی دارد؛ مثلاً:
• وقتی a کوچک تر از یک است، با افزایشِ x مقدار y کاهش می یابد.
• وقتی a بزرگتر از یک است، با افزایشِ x مقدار y افزایش می یابد.
توابع نمایی در زمینه هایی چون اقتصاد و زیست شناسی کاربردهای فراوانی دارد. از این رو، توابع نمایی و مسائل مربوط به رشد و زوال می توانند برای نمایش کاربردهای ریاضی در مسائل زندگی واقعی سودمند باشند.
برای تابع e x می توان کسری را به صورت زیر معرفی کرد:
e x = 1 + x 1 − x x + 2 − 2 x x + 3 − 3 x x + 4 − ⋱
یک هنرمند درخت چوبی را با استفاده از تعدادی قطعهٔ چوب شاخه مانند ساخته است. به این ترتیب، روی دسته های شاخهٔ اصلی شاخه هایِ دیگری ساخت و این کار را تا هشت سطح ادامه داد. جدول عملکرد وی به صورت زیر است:
رابطهٔ بین توان و تعداد شاخه ها برابر است با:
۲ به توان ۸ =۲۵۶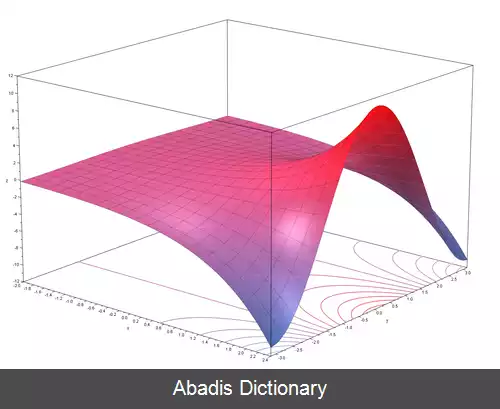
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر واقع، تابع لگاریتم عکس تابع نمایی است.
البته، این تابع را می توان به صورت a x نیز تعریف کرد. استفاده از لگاریتم نشان می دهد که:
این تابع را تابع نمایی با پایهٔ a می خوانیم که a عددی ثابت است.
در بسیاری از علوم وقتی از تابع نمایی صحبت می شود، منظور تابع k a x است.
عموماً متغیر x می تواند هر عدد حقیقی یا مختلط باشد. به عبارت دیگر، معکوس ln ( y ) = x را exp ( x ) = e x = y گویند.
تابع a − x قرینه تابع a x می باشد.
y = a − x = ( 1 a ) x
نکته: این دو تابع نسبت به محور yها قرینه یکدیگر هستند.
تابع − a x قرینه تابع a x می باشد.
نکته: این دو تابع نسبت به محور Xها قرینه یکدیگر هستند.
• تابع نمایی معکوسِ تابع لگاریتم طبیعی ( Y=ln ( x است.
• دامنه آن تمام اعداد حقیقی است.
• برد آن تمام اعداد مثبت است.
• مشتق آن همواره با خودش برابر یا بزرگ تر و تابعی پیوسته و صعودی از x است.
نمودار تابع نمایی دو حالت کلّی دارد؛ مثلاً:
• وقتی a کوچک تر از یک است، با افزایشِ x مقدار y کاهش می یابد.
• وقتی a بزرگتر از یک است، با افزایشِ x مقدار y افزایش می یابد.
توابع نمایی در زمینه هایی چون اقتصاد و زیست شناسی کاربردهای فراوانی دارد. از این رو، توابع نمایی و مسائل مربوط به رشد و زوال می توانند برای نمایش کاربردهای ریاضی در مسائل زندگی واقعی سودمند باشند.
برای تابع e x می توان کسری را به صورت زیر معرفی کرد:
e x = 1 + x 1 − x x + 2 − 2 x x + 3 − 3 x x + 4 − ⋱
یک هنرمند درخت چوبی را با استفاده از تعدادی قطعهٔ چوب شاخه مانند ساخته است. به این ترتیب، روی دسته های شاخهٔ اصلی شاخه هایِ دیگری ساخت و این کار را تا هشت سطح ادامه داد. جدول عملکرد وی به صورت زیر است:
رابطهٔ بین توان و تعداد شاخه ها برابر است با:
۲ به توان ۸ =۲۵۶





wiki: تابع نمایی
