در ریاضیات، تابع موج کولن حل معادله موج کولن است که به نام چارلز آگوستین دو کولن نامگذاری شده است. آنها برای توصیف رفتار ذرات باردار در یک پتانسیل کولن استفاده می شوند و می توانند بر اساس توابع ابر هندسی متقابل یا توابع ویتاکر بر حسب استدلال خیالی نوشته شوند.
معادله موج کولن برای یک ذره باردار با جرم معادله شرودینگر با پتانسیل کولن است
( − ℏ 2 ∇ 2 2 m + Z ℏ c α r ) ψ k → ( r → ) = ℏ 2 k 2 2 m ψ k → ( r → ) ,
جایی که حاصل ضرب بارهای ذره و منبع میدان است ( بر حسب واحد بار اولیه، برای اتم هیدروژن ) ثابت ساختار ریز است و انرژی ذره است. جوابی که تابع موج کولن است را می توان با حل این معادله در مختصات سهموی پیدا کرد.
بسته به شرایط مرزی انتخاب شده، راه حل اشکال مختلفی دارد. دو مورد از راه حل ها عبارتند از
جایی که تابع M ( a , b , z ) ≡ 1 F 1 ( a ; b ; z ) ابر هندسی همرو است، و η = Z m c α / ( ℏ k ) و Γ ( z ) تابع گاما است. دو شرط مرزی مورد استفاده در اینجا عبارتند از
که مطابقت دارند حالت مجانبی موج صفحه گرا به ترتیب قبل یا بعد از نزدیک شدن به منبع میدان در مبدأ. توابع با فرمول به یکدیگر مرتبط هستند
تابع موج ψ k → ( r → ) را می توان به امواج جزئی گسترش داد ( یعنی با توجه به پایه زاویه ای ) برای به دست آوردن توابع شعاعی مستقل از زاویه w ℓ ( η , ρ ) . اینجا ρ = k r .
ψ k → ( r → ) = 4 π r ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ i ℓ w ℓ ( η , ρ ) Y ℓ m ( r ^ ) Y ℓ m ∗ ( k ^ ) .
یک جمله منفرد از انبساط را می توان توسط محصول اسکالر با هارمونیک کروی خاص جدا کرد
ψ k ℓ m ( r → ) = ∫ ψ k → ( r → ) Y ℓ m ( k ^ ) d k ^ = R k ℓ ( r ) Y ℓ m ( r ^ ) , R k ℓ ( r ) = 4 π i ℓ w ℓ ( η , ρ ) / r .
معادله تک موج جزئی می توان با بازنویسی لاپلاسین در معادله موج کولن در مختصات کروی و طرح معادله بر روی یک هارمونیک کروی خاص به دست آورد. Y ℓ m ( r ^ )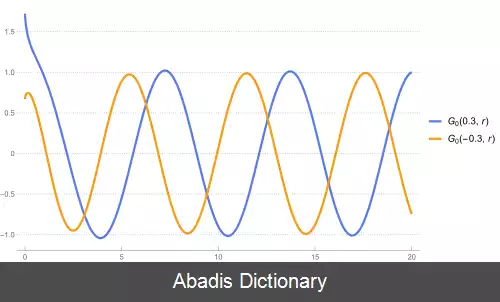
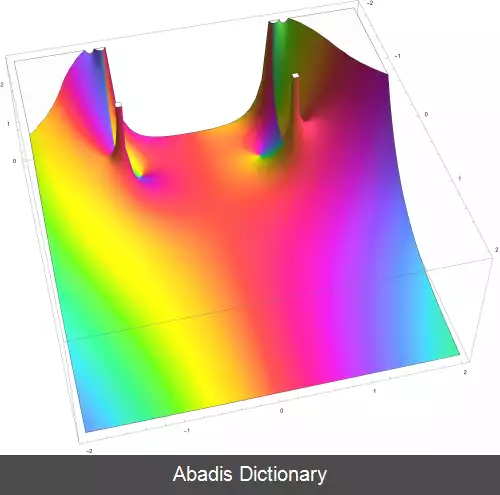
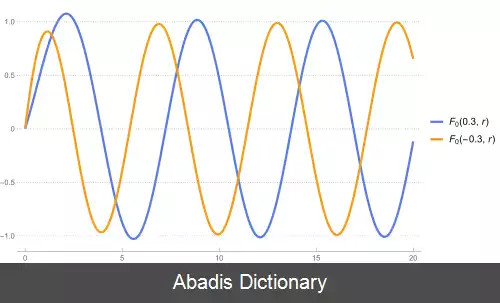
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعادله موج کولن برای یک ذره باردار با جرم معادله شرودینگر با پتانسیل کولن است
( − ℏ 2 ∇ 2 2 m + Z ℏ c α r ) ψ k → ( r → ) = ℏ 2 k 2 2 m ψ k → ( r → ) ,
جایی که حاصل ضرب بارهای ذره و منبع میدان است ( بر حسب واحد بار اولیه، برای اتم هیدروژن ) ثابت ساختار ریز است و انرژی ذره است. جوابی که تابع موج کولن است را می توان با حل این معادله در مختصات سهموی پیدا کرد.
بسته به شرایط مرزی انتخاب شده، راه حل اشکال مختلفی دارد. دو مورد از راه حل ها عبارتند از
جایی که تابع M ( a , b , z ) ≡ 1 F 1 ( a ; b ; z ) ابر هندسی همرو است، و η = Z m c α / ( ℏ k ) و Γ ( z ) تابع گاما است. دو شرط مرزی مورد استفاده در اینجا عبارتند از
که مطابقت دارند حالت مجانبی موج صفحه گرا به ترتیب قبل یا بعد از نزدیک شدن به منبع میدان در مبدأ. توابع با فرمول به یکدیگر مرتبط هستند
تابع موج ψ k → ( r → ) را می توان به امواج جزئی گسترش داد ( یعنی با توجه به پایه زاویه ای ) برای به دست آوردن توابع شعاعی مستقل از زاویه w ℓ ( η , ρ ) . اینجا ρ = k r .
ψ k → ( r → ) = 4 π r ∑ ℓ = 0 ∞ ∑ m = − ℓ ℓ i ℓ w ℓ ( η , ρ ) Y ℓ m ( r ^ ) Y ℓ m ∗ ( k ^ ) .
یک جمله منفرد از انبساط را می توان توسط محصول اسکالر با هارمونیک کروی خاص جدا کرد
ψ k ℓ m ( r → ) = ∫ ψ k → ( r → ) Y ℓ m ( k ^ ) d k ^ = R k ℓ ( r ) Y ℓ m ( r ^ ) , R k ℓ ( r ) = 4 π i ℓ w ℓ ( η , ρ ) / r .
معادله تک موج جزئی می توان با بازنویسی لاپلاسین در معادله موج کولن در مختصات کروی و طرح معادله بر روی یک هارمونیک کروی خاص به دست آورد. Y ℓ m ( r ^ )



wiki: تابع موج کولن
