تابع مستطیلی ( که با تابع مستطیل، تابع دروازه، پالس واحد و . . . نیز شناخته می شود ) به شکل زیر تعریف شده است:
این تابع، یک تابع پله ساده است. تعریف های دیگری نیز وجود دارد که r e c t ( ± 1 2 ) را 0، 1، یا نامعین می داند. ما نیز تابع مستطیلی را بر اساس تابع پله ای هویساید بیان می کنیم:
یا به عنوان جایگزین:
در حالت کلی تر:
تبدیل فوریه واحد تابع پله ای به صورت زیر خواهد بود:
و
که s i n c شکل نرمال شده آن است.
دقت کنید تا زمانی که تعریف تابع پالس به شکل دامنه - زمان آن مرتبط است، دلیلی برای اعتقاد داشتن به ظاهر نوسانی ( تابع تبدیل فوریه ) آن نیست. ولی، برخی از جنبه های تئوریک که باید کاملاً روشن باشد، مثل پهنای باند نامحدود، به ایجاد لبه های تیز نامعین در تعریف دامنه - زمان منجر می شود.
ما می توانیم تابع مثلثی را شکنج ( convolution ) دو تابع مستطیلی تعریف کنیم:
با مشاهده تابع مستطیلی به عنوان یک تابع توزیع احتمال، معادله مشخصه آن به شکل زیر خواهد بود:
و تابع تولید ممان آن نیز
خواهد بود که s i n h ( t ) , تابع سینوس هایپربولیک است.
• تابع پله
• تابع مثلثی
• تبدیل فوریه
• موج مربعی
• توابع خاص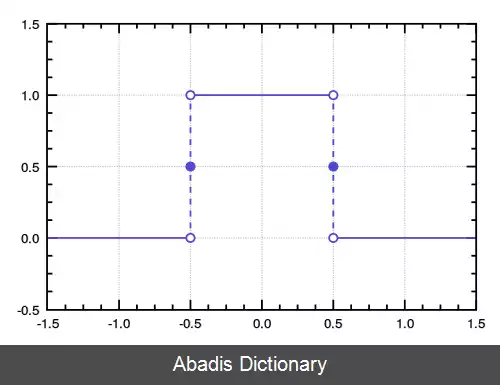
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین تابع، یک تابع پله ساده است. تعریف های دیگری نیز وجود دارد که r e c t ( ± 1 2 ) را 0، 1، یا نامعین می داند. ما نیز تابع مستطیلی را بر اساس تابع پله ای هویساید بیان می کنیم:
یا به عنوان جایگزین:
در حالت کلی تر:
تبدیل فوریه واحد تابع پله ای به صورت زیر خواهد بود:
و
که s i n c شکل نرمال شده آن است.
دقت کنید تا زمانی که تعریف تابع پالس به شکل دامنه - زمان آن مرتبط است، دلیلی برای اعتقاد داشتن به ظاهر نوسانی ( تابع تبدیل فوریه ) آن نیست. ولی، برخی از جنبه های تئوریک که باید کاملاً روشن باشد، مثل پهنای باند نامحدود، به ایجاد لبه های تیز نامعین در تعریف دامنه - زمان منجر می شود.
ما می توانیم تابع مثلثی را شکنج ( convolution ) دو تابع مستطیلی تعریف کنیم:
با مشاهده تابع مستطیلی به عنوان یک تابع توزیع احتمال، معادله مشخصه آن به شکل زیر خواهد بود:
و تابع تولید ممان آن نیز
خواهد بود که s i n h ( t ) , تابع سینوس هایپربولیک است.
• تابع پله
• تابع مثلثی
• تبدیل فوریه
• موج مربعی
• توابع خاص

wiki: تابع مستطیلی
