تابع مثلثی ( یا تابع کلاه یا تابع مثلث ) به صورت زیر تعریف می شود:
∧ ( t ) = { 1 − | t | , | t | < 1 0 , else
هم چنین می توان این تابع را به صورت کانولوشن تابع مستطیلی در خودش تعریف کرد:
∧ ( t ) = Π ( t ) ⋆ Π ( t ) = ∫ − ∞ + ∞ Π ( τ ) Π ( t − τ ) d τ
بنابراین این تابع را می توان به صورت تابع شیب ( انتگرال تابع پلهٔ واحد ) نیز نمایش داد:
∧ ( t ) = u − 2 ( t − 1 ) − 2 u − 2 ( t ) + u − 2 ( t + 1 )
این تابع در پردازش سیگنال و سیستم های مخابراتی از اهمیت بالایی برخوردار است.
تبدیل فوریه ی این سیگنال، مربع تابع سینک است. این امر را می توان هم از تعریف تبدیل فوریه و هم از خاصیت کانولوشن آن به دست آورد:
F { ∧ ( t ) } = F { Π ( t ) ⋆ Π ( t ) } = F { Π ( t ) } × F { Π ( t ) } = s i n c 2 ( f )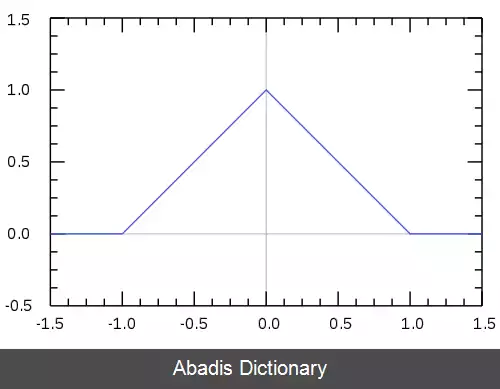
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف∧ ( t ) = { 1 − | t | , | t | < 1 0 , else
هم چنین می توان این تابع را به صورت کانولوشن تابع مستطیلی در خودش تعریف کرد:
∧ ( t ) = Π ( t ) ⋆ Π ( t ) = ∫ − ∞ + ∞ Π ( τ ) Π ( t − τ ) d τ
بنابراین این تابع را می توان به صورت تابع شیب ( انتگرال تابع پلهٔ واحد ) نیز نمایش داد:
∧ ( t ) = u − 2 ( t − 1 ) − 2 u − 2 ( t ) + u − 2 ( t + 1 )
این تابع در پردازش سیگنال و سیستم های مخابراتی از اهمیت بالایی برخوردار است.
تبدیل فوریه ی این سیگنال، مربع تابع سینک است. این امر را می توان هم از تعریف تبدیل فوریه و هم از خاصیت کانولوشن آن به دست آورد:
F { ∧ ( t ) } = F { Π ( t ) ⋆ Π ( t ) } = F { Π ( t ) } × F { Π ( t ) } = s i n c 2 ( f )

wiki: تابع مثلثی
