تابع فعال سازی Swish. تابع Swish به شکل زیر تعریف می شود:
[ ۱] swish ( x ) = x sigmoid ( β x ) = x 1 + e − β x .
که β می تواند ثابت، یا پارامتر قابل یادگیری باشد. اگر β = 1 باشد، تابع swish تبدیل به تابع سیگموئید خطی یا SiLU می شود.
• در حالت β → + ∞ {\displaystyle \beta \to +\infty } تابع به ReLU یا m a x ( x , 0 ) {\displaystyle max ( x, 0 ) } تبدیل می شود.
• در حالت β → 0 {\displaystyle \beta \to 0} تابع حاصل خطی و برابر با x 2 {\displaystyle {\frac {x}{2}}}
• در حالت β → − ∞ {\displaystyle \beta \to - \infty } تابع به m i n ( x , 0 ) {\displaystyle min ( x, 0 ) } تبدیل می شود.
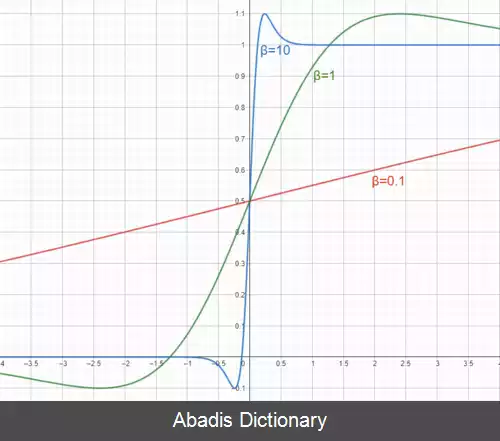
مشتق تابع swish نسبت به x بدین شکل قابل محاسبه است:
f ′ ( x ) = σ ( β x ) + β x ⋅ σ ( β x ) ( 1 − σ ( β x ) ) = σ ( β x ) + β x ⋅ σ ( β x ) − β x ⋅ σ ( β x ) 2 = β x ⋅ σ ( β x ) + σ ( β x ) ( 1 − β x ⋅ σ ( β x ) ) = β f ( x ) + σ ( β x ) ( 1 − β f ( x ) )
مشتق تابع swish نسبت به β بدین شکل قابل محاسبه است: ∂ f ( x ) ∂ β = x 2 σ ( β x ) ( 1 − σ ( β x ) )
در سال 2017 دانشمندان در Google توانستند با جایگزینی تابع swish به جای ReLU و Sigmoid، نتایج بهتری برای دیتاست ایمیج نت بدست آورند. همچنین عملکرد این تابع در سایر مدل ها و دیتاست های مشهور برابر یا بهتر از دیگر توابع فعال سازی رایح بوده است. البته باید توجه داشت که تابع swish نسبت به ReLU از لحاظ محاسبات چه در محاسبه تابع و چه در محاسبه مشتق بسیار پیچیده تر است. [ ۲]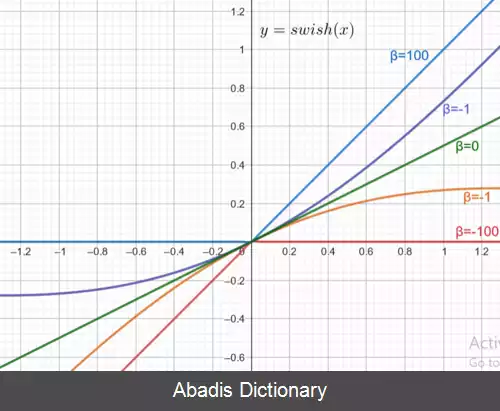
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف[ ۱] swish ( x ) = x sigmoid ( β x ) = x 1 + e − β x .
که β می تواند ثابت، یا پارامتر قابل یادگیری باشد. اگر β = 1 باشد، تابع swish تبدیل به تابع سیگموئید خطی یا SiLU می شود.
• در حالت β → + ∞ {\displaystyle \beta \to +\infty } تابع به ReLU یا m a x ( x , 0 ) {\displaystyle max ( x, 0 ) } تبدیل می شود.
• در حالت β → 0 {\displaystyle \beta \to 0} تابع حاصل خطی و برابر با x 2 {\displaystyle {\frac {x}{2}}}
• در حالت β → − ∞ {\displaystyle \beta \to - \infty } تابع به m i n ( x , 0 ) {\displaystyle min ( x, 0 ) } تبدیل می شود.
مشتق تابع swish نسبت به x بدین شکل قابل محاسبه است:
f ′ ( x ) = σ ( β x ) + β x ⋅ σ ( β x ) ( 1 − σ ( β x ) ) = σ ( β x ) + β x ⋅ σ ( β x ) − β x ⋅ σ ( β x ) 2 = β x ⋅ σ ( β x ) + σ ( β x ) ( 1 − β x ⋅ σ ( β x ) ) = β f ( x ) + σ ( β x ) ( 1 − β f ( x ) )
مشتق تابع swish نسبت به β بدین شکل قابل محاسبه است: ∂ f ( x ) ∂ β = x 2 σ ( β x ) ( 1 − σ ( β x ) )
در سال 2017 دانشمندان در Google توانستند با جایگزینی تابع swish به جای ReLU و Sigmoid، نتایج بهتری برای دیتاست ایمیج نت بدست آورند. همچنین عملکرد این تابع در سایر مدل ها و دیتاست های مشهور برابر یا بهتر از دیگر توابع فعال سازی رایح بوده است. البته باید توجه داشت که تابع swish نسبت به ReLU از لحاظ محاسبات چه در محاسبه تابع و چه در محاسبه مشتق بسیار پیچیده تر است. [ ۲]


wiki: تابع فعال سازی Swish
