در ریاضیات، تابع علامت تابعی فرد است که علامت یک عدد حقیقی را بدست می دهد. در ریاضی با نماد sgn کاربرد دارد که کوتاه نوشتی برای sign به معنی علامت است، چرا که، اعداد را بر حسب علامتشان جدا می کند. این تابع نمونه ای از توابع چند ضابطه ای است.
تابع علامت برای عدد حقیقی x به صورت زیر تعریف می شود:
هر عدد حقیقی را می توان به صورت حاصل ضرب قدر مطلق آن در تابع علامتش نوشت:
از معادلهٔ بالا چنین بدست می آید که هرگاه x ناصفر باشد تابع علامت آن را می توان به صورت زیر بازنویسی کرد:
و البته برای تمامی اعداد حقیقی x می توان گفت:
تابع علامت مشتق تابع قدر مطلق نیز است ( تا سر نامعینی در صفر ) :
آنچه باقی می ماند تنها علامت x است.
تابع علامت در همه جا جز صفر، مشتق پذیر است و مقدار مشتق آن برابر صفر است. این تابع در حالت عادی در نقطهٔ صفر مشتق پذیر نیست ولی در شرایط مفهوم عمومی مشتق گیری در نظریهٔ توزیع، مشتق تابع علامت برابر است با دو برابر تابع دلتای دیراک که برای بیان آن می توان از رابطهٔ زیر بهره برد:[ ۱]
که در آن H ( x ) تابع پله ای هویساید است و H ( ۰ ) = ۱/۲ می باشد. با کمک این برابری دوباره مشتق گیری می کنیم:[ ۲]
می توان تابع علامت را به کمک براکت ایورسون هم نوشت:
که در آن k ≫ 1 ، تقریب مناسبی برای تابع علامت به صورت زیر است:
تقریب دیگر چنین است:
که برای ϵ → 0 مقدار آن نزدیک تر به دقیق می شود. یادآوری می شود که این رابطه مشتق x 2 + ϵ 2 است. این مطلب از آنجا بدست آمده که: رابطهٔ بالا در صورت صفر بودن ϵ برای تمام xهای ناصفر رابطه ای دقیق است و مانند تعمیم دادن تابع علامت در بُعدهای دیگر می ماند ( مانند مشتق جزئی x 2 + y 2 ) .
نگاه کنید به مقالهٔ تابع پله ای هویساید.
تابع علامت را می توان تا مجموعهٔ اعداد مختلط هم گسترش داد؛ به این ترتیب:
که در آن z عضو C است مگر در نقطهٔ صفر. تابع علامت عدد دلخواه z در مجموعهٔ اعداد مختلط، برابر با نقطه ای است روی دایره واحد یک صفحهٔ مختلط که در نزدیک ترین فاصله به z قرار دارد. پس برای zهای ناصفر داریم:
در این رابطه arg همان زاویهٔ φ در بیان قطبی عدد مختلط است. توضیح: اگر یک عدد مختلط را به صورت r ( cos ϕ + i sin ϕ ) یا r e i ϕ نمایش دهیم، arg همان زاویهٔ φ است. به دلیل تقارن و همچنین برای آنکه تابع را به تمامی تعمیم داده باشیم، برای نقطهٔ 0 = z تابع را چنین نشان می دهیم: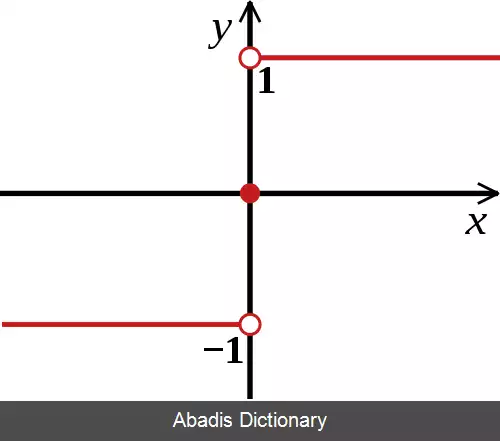
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع علامت برای عدد حقیقی x به صورت زیر تعریف می شود:
هر عدد حقیقی را می توان به صورت حاصل ضرب قدر مطلق آن در تابع علامتش نوشت:
از معادلهٔ بالا چنین بدست می آید که هرگاه x ناصفر باشد تابع علامت آن را می توان به صورت زیر بازنویسی کرد:
و البته برای تمامی اعداد حقیقی x می توان گفت:
تابع علامت مشتق تابع قدر مطلق نیز است ( تا سر نامعینی در صفر ) :
آنچه باقی می ماند تنها علامت x است.
تابع علامت در همه جا جز صفر، مشتق پذیر است و مقدار مشتق آن برابر صفر است. این تابع در حالت عادی در نقطهٔ صفر مشتق پذیر نیست ولی در شرایط مفهوم عمومی مشتق گیری در نظریهٔ توزیع، مشتق تابع علامت برابر است با دو برابر تابع دلتای دیراک که برای بیان آن می توان از رابطهٔ زیر بهره برد:[ ۱]
که در آن H ( x ) تابع پله ای هویساید است و H ( ۰ ) = ۱/۲ می باشد. با کمک این برابری دوباره مشتق گیری می کنیم:[ ۲]
می توان تابع علامت را به کمک براکت ایورسون هم نوشت:
که در آن k ≫ 1 ، تقریب مناسبی برای تابع علامت به صورت زیر است:
تقریب دیگر چنین است:
که برای ϵ → 0 مقدار آن نزدیک تر به دقیق می شود. یادآوری می شود که این رابطه مشتق x 2 + ϵ 2 است. این مطلب از آنجا بدست آمده که: رابطهٔ بالا در صورت صفر بودن ϵ برای تمام xهای ناصفر رابطه ای دقیق است و مانند تعمیم دادن تابع علامت در بُعدهای دیگر می ماند ( مانند مشتق جزئی x 2 + y 2 ) .
نگاه کنید به مقالهٔ تابع پله ای هویساید.
تابع علامت را می توان تا مجموعهٔ اعداد مختلط هم گسترش داد؛ به این ترتیب:
که در آن z عضو C است مگر در نقطهٔ صفر. تابع علامت عدد دلخواه z در مجموعهٔ اعداد مختلط، برابر با نقطه ای است روی دایره واحد یک صفحهٔ مختلط که در نزدیک ترین فاصله به z قرار دارد. پس برای zهای ناصفر داریم:
در این رابطه arg همان زاویهٔ φ در بیان قطبی عدد مختلط است. توضیح: اگر یک عدد مختلط را به صورت r ( cos ϕ + i sin ϕ ) یا r e i ϕ نمایش دهیم، arg همان زاویهٔ φ است. به دلیل تقارن و همچنین برای آنکه تابع را به تمامی تعمیم داده باشیم، برای نقطهٔ 0 = z تابع را چنین نشان می دهیم:

wiki: تابع علامت
