تابع شیب ( ramp function ) یک تابع حقیقی است، که شکل منحنی آن مانند سطح شیب دار است. آن را می توان با تعاریف متعددی بیان کرد، به عنوان مثال برای ورودی های منفی مقدار خروجی صفر است و برای ورودی های غیر منفی، خروجی با ورودی برابر است. عبارت شیب همچنین می تواند برای سایر توابع بدست آمده از طریق تغییر مقیاس و انتقال دهی استفاده شود و این تابع در این مقاله تابع شیب واحد است ( شیب ۱ با شروع از ۰ ) .
این تابع کاربردهای بی شماری در ریاضیات و مهندسی دارد و بسته به متن به اسامی مختلفی به کار می رود.
تابع شیب ( +R ( x ) : ℝ → ℝ 0 ) ممکن است از چند طریق به صورت تحلیلی تعریف شود. تعاریف ممکن عبارتند از:
• یک تابع چند ضابطه ای: R ( x ) := { x , x ≥ 0 ; 0 , x < 0 {\displaystyle R ( x ) :={\begin{cases}x, & x\geq 0; \\0, & x< 0\end{cases}}}
• تابع حداکثر: R ( x ) := max ( x , 0 ) {\displaystyle R ( x ) :=\max ( x, 0 ) }
• میانگینِ یک متغیر مستقل و مقدار قدر مطلق آن ( یک خط مستقیم با شیب واحد و مدول آن ) : R ( x ) := x + | x | 2 {\displaystyle R ( x ) :={\frac {x+|x|}{2}}}
• تابع پله هویساید ضرب شده به یک خط مستقیم با گرادیان واحد: R ( x ) := x H ( x ) {\displaystyle R\left ( x\right ) :=xH ( x ) }
• کانولوشنِ تابع پله هویساید با خود: R ( x ) := H ( x ) ∗ H ( x ) {\displaystyle R\left ( x\right ) :=H ( x ) *H ( x ) }
• انتگرال تابع پله هویساید:[ ۱] R ( x ) := ∫ − ∞ x H ( ξ ) d ξ {\displaystyle R ( x ) :=\int _{ - \infty }^{x}H ( \xi ) \, d\xi }
• براکت مَکالی: R ( x ) := ⟨ x ⟩ {\displaystyle R ( x ) :=\langle x\rangle }
تابع شیب کاربردهای بی شماری در مهندسی دارد، مانند تئوری پردازش سیگنال دیجیتال.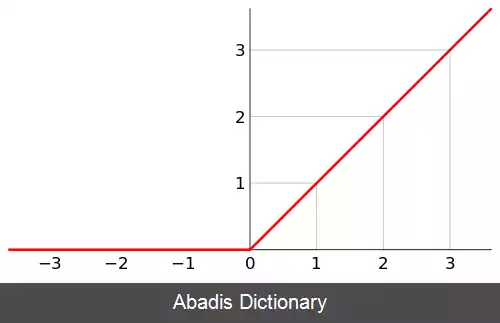
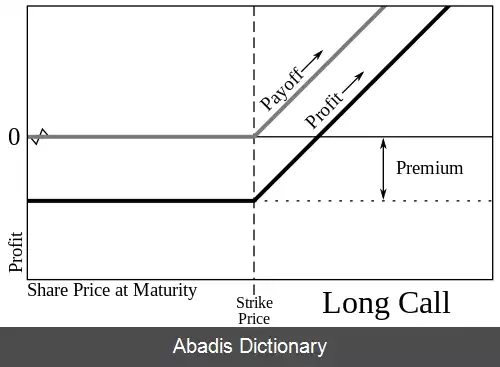
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین تابع کاربردهای بی شماری در ریاضیات و مهندسی دارد و بسته به متن به اسامی مختلفی به کار می رود.
تابع شیب ( +R ( x ) : ℝ → ℝ 0 ) ممکن است از چند طریق به صورت تحلیلی تعریف شود. تعاریف ممکن عبارتند از:
• یک تابع چند ضابطه ای: R ( x ) := { x , x ≥ 0 ; 0 , x < 0 {\displaystyle R ( x ) :={\begin{cases}x, & x\geq 0; \\0, & x< 0\end{cases}}}
• تابع حداکثر: R ( x ) := max ( x , 0 ) {\displaystyle R ( x ) :=\max ( x, 0 ) }
• میانگینِ یک متغیر مستقل و مقدار قدر مطلق آن ( یک خط مستقیم با شیب واحد و مدول آن ) : R ( x ) := x + | x | 2 {\displaystyle R ( x ) :={\frac {x+|x|}{2}}}
• تابع پله هویساید ضرب شده به یک خط مستقیم با گرادیان واحد: R ( x ) := x H ( x ) {\displaystyle R\left ( x\right ) :=xH ( x ) }
• کانولوشنِ تابع پله هویساید با خود: R ( x ) := H ( x ) ∗ H ( x ) {\displaystyle R\left ( x\right ) :=H ( x ) *H ( x ) }
• انتگرال تابع پله هویساید:[ ۱] R ( x ) := ∫ − ∞ x H ( ξ ) d ξ {\displaystyle R ( x ) :=\int _{ - \infty }^{x}H ( \xi ) \, d\xi }
• براکت مَکالی: R ( x ) := ⟨ x ⟩ {\displaystyle R ( x ) :=\langle x\rangle }
تابع شیب کاربردهای بی شماری در مهندسی دارد، مانند تئوری پردازش سیگنال دیجیتال.


wiki: تابع شیب
