در ریاضیات تابع شمارش اعداد اول تابعی است که برای بیان تعداد اعداد اول به کار می رود و آن را با نماد π ( x ) نمایش می دهند.
در قرن ۱۸ گاوس و لژاندر توانستند تقریب دقیق x / ln ( x ) را برای تعداد اعداد اول به دست آورند که بعدها این تقریب به نظریه اعداد اول مشهور شد و بر اساس آن ثابت شد که:
lim x → ∞ π ( x ) x / ln ( x ) = 1.
با تعریف تابع انتگرال لگاریتم که آن را با نماد l i ( x ) نمایش می دهند و به صورت زیر تعریف می شود:
l i ( x ) = ∫ 0 x d t ln t .
ثابت شد که:
lim x → ∞ π ( x ) / li ( x ) = 1
همانطور که مشاهده می شود اعداد به ۱ نزدیک می شوند.
ریاضیدان فرانسوی پیر دوسارارت ثابت کرد که برای x ≥ ۵۹۹ رابطه زیر برقرار است:
x ln x ( 1 + 1 ln x ) < π ( x ) < x ln x ( 1 + 1 ln x + 2. 51 ( ln x ) 2 ) .
همچنین ثابت کرد که برای هر x ≥ ۳۵۵۹۹۱:
x ln x + 2 < π ( x ) < x ln x − 4
بعدها ثابت شد که برای هر ε> ۰ وجود دارد عددی طبیعی ماننده s که برای هر x> s رابطه زیر برقرار است:
x ln x − ( 1 − ε ) < π ( x ) < x ln x − ( 1 + ε ) .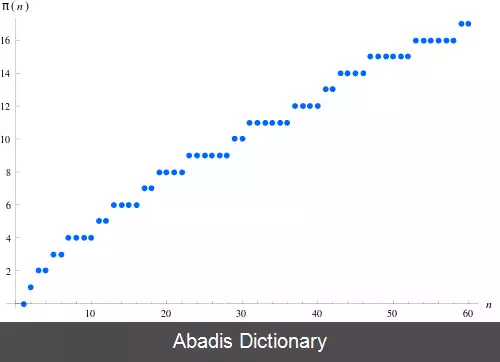
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر قرن ۱۸ گاوس و لژاندر توانستند تقریب دقیق x / ln ( x ) را برای تعداد اعداد اول به دست آورند که بعدها این تقریب به نظریه اعداد اول مشهور شد و بر اساس آن ثابت شد که:
lim x → ∞ π ( x ) x / ln ( x ) = 1.
با تعریف تابع انتگرال لگاریتم که آن را با نماد l i ( x ) نمایش می دهند و به صورت زیر تعریف می شود:
l i ( x ) = ∫ 0 x d t ln t .
ثابت شد که:
lim x → ∞ π ( x ) / li ( x ) = 1
همانطور که مشاهده می شود اعداد به ۱ نزدیک می شوند.
ریاضیدان فرانسوی پیر دوسارارت ثابت کرد که برای x ≥ ۵۹۹ رابطه زیر برقرار است:
x ln x ( 1 + 1 ln x ) < π ( x ) < x ln x ( 1 + 1 ln x + 2. 51 ( ln x ) 2 ) .
همچنین ثابت کرد که برای هر x ≥ ۳۵۵۹۹۱:
x ln x + 2 < π ( x ) < x ln x − 4
بعدها ثابت شد که برای هر ε> ۰ وجود دارد عددی طبیعی ماننده s که برای هر x> s رابطه زیر برقرار است:
x ln x − ( 1 − ε ) < π ( x ) < x ln x − ( 1 + ε ) .

wiki: تابع شمارش اعداد اول
