در ریاضیات، تابع سینک ( که با ( sinc ( x و گاهی با ( Sa ( x نشان داده می شود ) دو تعریف نسبتاً معادل همدیگر دارد. در پردازش سیگنال رقمی و نظریه اطلاعات تابع سینک نرمال شده معمولاً با رابطه زیر تعریف می شود:
این تعریف نام نرمال شده را به این دلیل یدک می کشد که انتگرالگیری بر روی تمام x به مقدار واحد منجر می شود. تبدیل فوریه تابع نرمال شده سینک با تابع مستطیلی شناخته می شود.
در ریاضیات تابع سینک غیر نرمال شده باستانی به صورت زیر تعریف می شود:
تنها تفاوت بین این دو تعریف مقیاس دهی متغیر مستقل ( همان محور x ) با عامل ضرب شونده π است. در هر دو حالت، مقدار تابع در ناتکینی قابل رفع در نقطه صفر گاهی به طور خاص در حد برابر با ۱ مشخص می شود. [ ۱] تابع سینک در همه جا تحلیلی است.
عبارت "sinc" که دارای تلفظ ( آوایش انگلیسی: /ˈsɪŋk/ ) است، از قطع انتهای تام لاتین کامل تابع که sinus cardinalis ( همان cardinal sine انگلیسی ) است بدست آمده است.
عبور از صفر ( zero crossing ) تابع سینک غیرنرمال شده در مضارب π؛ تلاقی با محور تابع سینک نرمال شده در اعداد صحیح غیر صفر.
نقاط ماکزیزم و مینیمم نسبی تابع سینک نرمال نشده متناظر است با نقاط تقاطع آن با تابع کسینوس. یعنی، ( sin ( ξ ) /ξ = cos ( ξ به ازای تمام ξهایی که مشتق sin ( x ) /x در آن ها صفر راست ( که در نتیجه به یک اکسترمم نسبی رسیده ایم ) .
تابع سینک نرمال شده دارای یک نمایش ساده در حالت ضرب نامحدود است:
و توسط فرمول انعکاس اولر با تابع گامای Γ مرتبط می شود:
لئونارد اویلر کشف کرد که
تبدیل فوریه پیوسته زمان تابع سینک نرمال شده ( نسبت به فرکانس معمولی ) ( rect ( f است،
که پاسخ تابع مستطیلی بین minus; 1/2& و 1/2 برابر 1 است، و در سایر مناطق برابر صفر است. این مسئله متناظر با ین واقعیت است که فیلتر سینک ( دیوار آجری یعنی پاسخ فرکانسی مربعی ) یک فیلتر پایین گذر ایده آل است. انتگرال فوریه مذکور، با در نظر گرفتن حالت خاص زیر
یک انتگرال اولیه است و یک انتگرال همگرای en:Lebesgue integral نیست
تابع سینک نرمال شده خواصی دارد که آن را در رابطه با میانیابی نمونه برداری توابع محدود باند ایده آل می سازد:
• این یک تابع میانیاب است، یعنی sinc ( 0 ) = 1 و برای kهای صحیح غیر صفر داریم sinc ( k ) = 0.
• تابع ( xk ( t ) = sinc ( t−k یک تابع پایه ارتونرمال برای توابع محدود باند در فضای تابع ( L2 ( R است، با فرکانس زاویه حداکثر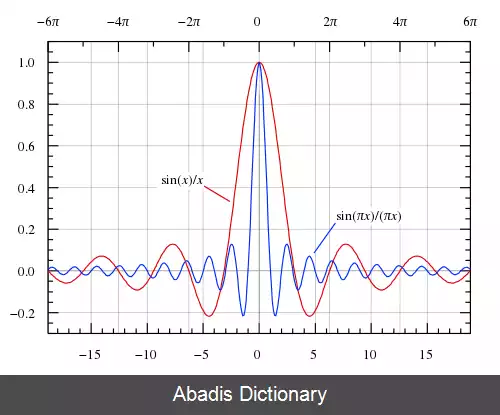
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین تعریف نام نرمال شده را به این دلیل یدک می کشد که انتگرالگیری بر روی تمام x به مقدار واحد منجر می شود. تبدیل فوریه تابع نرمال شده سینک با تابع مستطیلی شناخته می شود.
در ریاضیات تابع سینک غیر نرمال شده باستانی به صورت زیر تعریف می شود:
تنها تفاوت بین این دو تعریف مقیاس دهی متغیر مستقل ( همان محور x ) با عامل ضرب شونده π است. در هر دو حالت، مقدار تابع در ناتکینی قابل رفع در نقطه صفر گاهی به طور خاص در حد برابر با ۱ مشخص می شود. [ ۱] تابع سینک در همه جا تحلیلی است.
عبارت "sinc" که دارای تلفظ ( آوایش انگلیسی: /ˈsɪŋk/ ) است، از قطع انتهای تام لاتین کامل تابع که sinus cardinalis ( همان cardinal sine انگلیسی ) است بدست آمده است.
عبور از صفر ( zero crossing ) تابع سینک غیرنرمال شده در مضارب π؛ تلاقی با محور تابع سینک نرمال شده در اعداد صحیح غیر صفر.
نقاط ماکزیزم و مینیمم نسبی تابع سینک نرمال نشده متناظر است با نقاط تقاطع آن با تابع کسینوس. یعنی، ( sin ( ξ ) /ξ = cos ( ξ به ازای تمام ξهایی که مشتق sin ( x ) /x در آن ها صفر راست ( که در نتیجه به یک اکسترمم نسبی رسیده ایم ) .
تابع سینک نرمال شده دارای یک نمایش ساده در حالت ضرب نامحدود است:
و توسط فرمول انعکاس اولر با تابع گامای Γ مرتبط می شود:
لئونارد اویلر کشف کرد که
تبدیل فوریه پیوسته زمان تابع سینک نرمال شده ( نسبت به فرکانس معمولی ) ( rect ( f است،
که پاسخ تابع مستطیلی بین minus; 1/2& و 1/2 برابر 1 است، و در سایر مناطق برابر صفر است. این مسئله متناظر با ین واقعیت است که فیلتر سینک ( دیوار آجری یعنی پاسخ فرکانسی مربعی ) یک فیلتر پایین گذر ایده آل است. انتگرال فوریه مذکور، با در نظر گرفتن حالت خاص زیر
یک انتگرال اولیه است و یک انتگرال همگرای en:Lebesgue integral نیست
تابع سینک نرمال شده خواصی دارد که آن را در رابطه با میانیابی نمونه برداری توابع محدود باند ایده آل می سازد:
• این یک تابع میانیاب است، یعنی sinc ( 0 ) = 1 و برای kهای صحیح غیر صفر داریم sinc ( k ) = 0.
• تابع ( xk ( t ) = sinc ( t−k یک تابع پایه ارتونرمال برای توابع محدود باند در فضای تابع ( L2 ( R است، با فرکانس زاویه حداکثر

wiki: تابع سینک
