تابع زتای ریمان
فرهنگستان زبان و ادب
دانشنامه عمومی
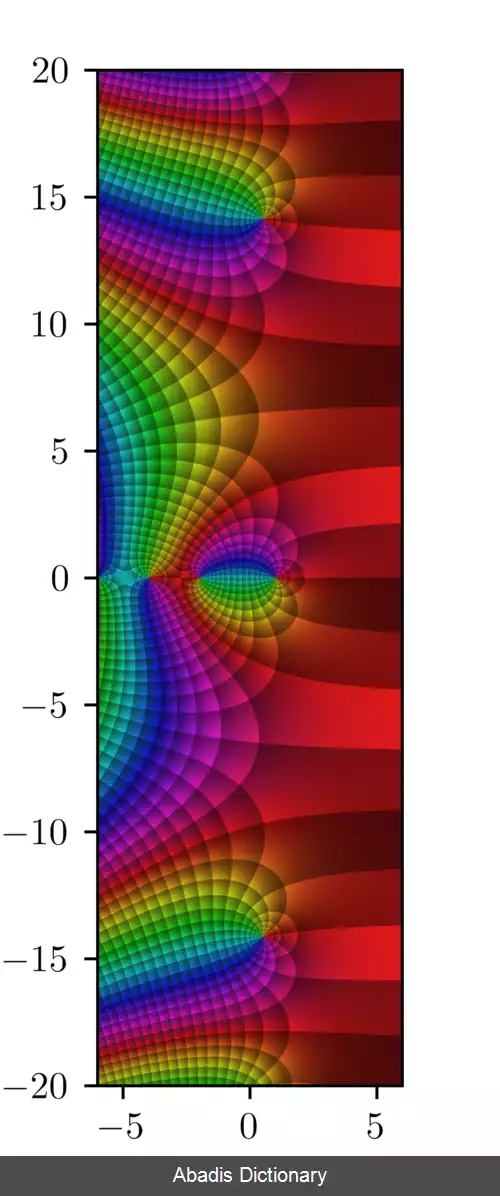
تابع زتای ریمان یا تابع زتای ریمان - اویلر، ζ ( s ) ، تابع ریاضیاتی از یک متغیر مختلط چون s است که می توان آن را به صورت زیر بیان نمود:
تابع زتای ریمان نقش مهمی در نظریه تحلیلی اعداد داشته و کاربردهایی در فیزیک، نظریه احتمالات، و آمار کاربردی دارد.
لئونارد اویلر اولین بار این تابع را در نیمه اول قرن هجدهم، تنها با استفاده از اعداد حقیقی معرفی و مطالعه نمود، چرا که آنالیز مختلط در آن زمان موجود نبود. مقاله ۱۸۵۹ برنهارت ریمان با عنوان «در مورد تعداد اعداد اول کوچکتر از مقداری داده شده»، تعریف اویلر را به یک متغیر مختلط بسط داده و پیوستگی مرومورفیک و معادله تابعی آن را اثبات نموده و رابطه ای بین صفرهایش و توزیع اعداد اول برقرار نمود. [ ۲]
مقادیر تابع زتای ریمان در اعداد صحیح مثبت زوج، توسط اویلر محاسبه شدند. اولین آن ها ζ ( 2 ) بود که حلی را برای مسئله بازل ارائه می کند. در ۱۹۷۹، راجر آپری گنگ بودن ζ ( 3 ) را اثبات نمود. مقادیر نقاط صحیح منفی نیز که توسط اویلر یافت شدند، اعداد گویا بوده و نقش مهمی را در نظریه فرم های مدولار ( پیمانه ای ) بازی می کنند. تعمیم های زیادی از تابع زتای ریمانی چون سری های دیریکله، L - توابع دیریکله و L - توابع نیز شناخته شده می باشند.
تابع زتای ریمان ζ ( s ) ، تابعی از متغیر مختلط s = σ + i t است. ( نمادهای s و σ و t را به طور سنتی و با پیروی از ریمان، در مطالعه این تابع استفاده می کنند ) هنگامی که R e ( s ) = σ > 1 ، زتای ریمان را می توان به صورت جمع همگرا یا انتگرال نوشت:
که در آن:
تابع گاما است. تابع زتای ریمان برای سایر مقادیر مختلط، از طریق ادامه تحلیلی در σ > 1 تعریف می گردد.
لئونارد اویلر سری بالا را در ۱۷۴۰ برای مقادیر مثبت صحیح s در نظر گرفت و سپس چبیشف تعریف را برای Re ( s ) > 1 نیز گسترش داد. [ ۳]
سری فوق نمونه اولیه ای از سری دیریکله است، چنانکه برای sهایی که σ > 1 باشند به طور مطلق به یک تابع تحلیلی همگرا بوده و برای سایر مقادیر s واگراست. ریمان نشان داد که تابع تعریف شده توسط این سری روی نیم صفحه بالایی را می توان به تمام مقادیر مختلطی که s ≠ 1 اند به صورت تحلیلی ادامه داد. برای s=۱، این سری تبدیل به سری هارمونیک شده که به ∞ واگرا بوده و: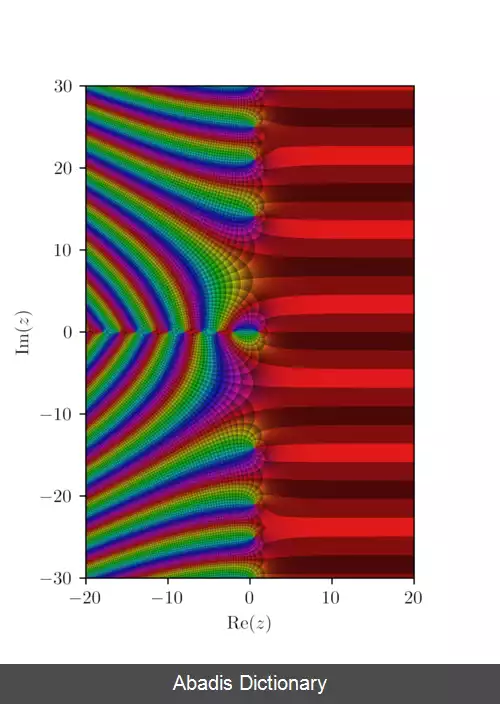

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع زتای ریمان نقش مهمی در نظریه تحلیلی اعداد داشته و کاربردهایی در فیزیک، نظریه احتمالات، و آمار کاربردی دارد.
لئونارد اویلر اولین بار این تابع را در نیمه اول قرن هجدهم، تنها با استفاده از اعداد حقیقی معرفی و مطالعه نمود، چرا که آنالیز مختلط در آن زمان موجود نبود. مقاله ۱۸۵۹ برنهارت ریمان با عنوان «در مورد تعداد اعداد اول کوچکتر از مقداری داده شده»، تعریف اویلر را به یک متغیر مختلط بسط داده و پیوستگی مرومورفیک و معادله تابعی آن را اثبات نموده و رابطه ای بین صفرهایش و توزیع اعداد اول برقرار نمود. [ ۲]
مقادیر تابع زتای ریمان در اعداد صحیح مثبت زوج، توسط اویلر محاسبه شدند. اولین آن ها ζ ( 2 ) بود که حلی را برای مسئله بازل ارائه می کند. در ۱۹۷۹، راجر آپری گنگ بودن ζ ( 3 ) را اثبات نمود. مقادیر نقاط صحیح منفی نیز که توسط اویلر یافت شدند، اعداد گویا بوده و نقش مهمی را در نظریه فرم های مدولار ( پیمانه ای ) بازی می کنند. تعمیم های زیادی از تابع زتای ریمانی چون سری های دیریکله، L - توابع دیریکله و L - توابع نیز شناخته شده می باشند.
تابع زتای ریمان ζ ( s ) ، تابعی از متغیر مختلط s = σ + i t است. ( نمادهای s و σ و t را به طور سنتی و با پیروی از ریمان، در مطالعه این تابع استفاده می کنند ) هنگامی که R e ( s ) = σ > 1 ، زتای ریمان را می توان به صورت جمع همگرا یا انتگرال نوشت:
که در آن:
تابع گاما است. تابع زتای ریمان برای سایر مقادیر مختلط، از طریق ادامه تحلیلی در σ > 1 تعریف می گردد.
لئونارد اویلر سری بالا را در ۱۷۴۰ برای مقادیر مثبت صحیح s در نظر گرفت و سپس چبیشف تعریف را برای Re ( s ) > 1 نیز گسترش داد. [ ۳]
سری فوق نمونه اولیه ای از سری دیریکله است، چنانکه برای sهایی که σ > 1 باشند به طور مطلق به یک تابع تحلیلی همگرا بوده و برای سایر مقادیر s واگراست. ریمان نشان داد که تابع تعریف شده توسط این سری روی نیم صفحه بالایی را می توان به تمام مقادیر مختلطی که s ≠ 1 اند به صورت تحلیلی ادامه داد. برای s=۱، این سری تبدیل به سری هارمونیک شده که به ∞ واگرا بوده و:



wiki: تابع زتای ریمان
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
