در بهینه سازی های ریاضی تابع روزن بروک تابع غیر محدب استفاده می شود که توسط هاوارد اچ روزن بروک در سال ۱۹۶۰ به عنوان یک آزمون عملکرد برای بهینه سازی الگوریتم ها معرفی شده است. [ ۱] همچنین به عنوان دره روزن بروک یا Rosenbrock's banana function شناخته می شود.
که هدف آن پیدا کردن مینیمم و بهینه کردن تابع سهمی وار شکل شده تخت
شکل کلی تابع اینگونه تعریف شده است:
f ( x , y ) = ( a − x ) 2 + b ( y − x 2 ) 2
نقطه مینیمم بهینه ( x , y ) = ( a , a 2 ) جایی که f ( x , y ) = 0 . که معمولاً a = 1 و b = 100 .
در دو نوع معمولاً اتفاق می افتد اولی مجموع N / 2 و دومی مشکلات غیر همراه 2D Rosenbrock
این نوع دیگر که تنها تعریف شده برای هر N و راه حل های ساده قابل پیش بینی.
A بیشتر درگیر نوع است
این نوع نشان داده شده است که دقیقاً یک حداقل N = 3 ( در ( 1 , 1 , 1 ) ) و دقیقاً دو کمترین برای 4 ≤ N ≤ 7 جهانی حداقل همه آنهایی که محلی حداقل در نزدیکی ( x 1 , x 2 , … , x N ) = ( − 1 , 1 , … , 1 ) . این نتیجه به دست آمده است با تنظیم شیب تابع برابر صفر توجه است که در نتیجه معادله یک تابع منطقی x است. برای N چندجمله ای تعیین می شود و دقیقاً قضیه استورم می تواند مورد استفاده برای تعیین تعداد ریشه های واقعی در حالی که ریشه ها را می توان محدود در منطقه | x i | < 2. 4 است. [ ۴] برای بزرگتر N این روش معافیت های پایین با توجه به اندازه ضرایب درگیر است.
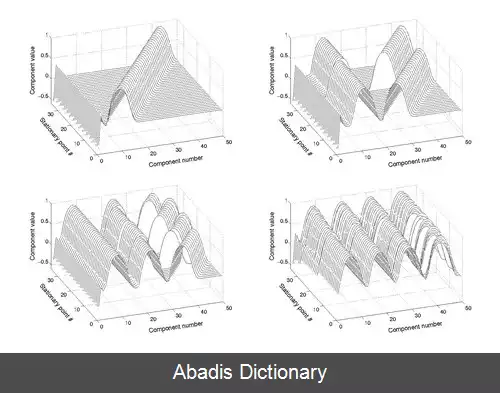
بسیاری از نقاط ثابت از تابع نشان یک الگوی منظم که رسم شده است؛ که این ساختار می تواند برای آن ها را بیابید.
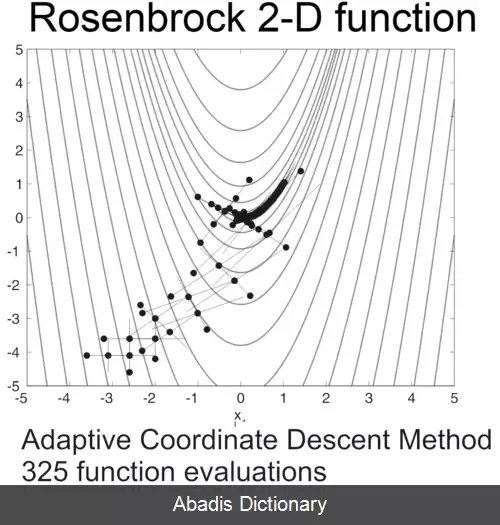
این تابع روزن بروک می تواند کارآمد بهینه سازی شده توسط تطبیق مناسب و هماهنگ کردن سیستم بدون استفاده از هر گونه شیب اطلاعات و بدون ساختمان محلی تقریب ( در مقایسه با بسیاری از derivate - رایگان بهینه ) . شکل زیر نشان می دهد به عنوان مثال از ۲ بعدی Rosenbrock تابع بهینه سازی توسط تطبیقی هماهنگ تبار از نقطه شروع x 0 = ( − 3 , − 4 ) . این راه حل با مقدار تابع را 10 − 10 می توان پس از ۳۲۵ تابع ارزیابی است.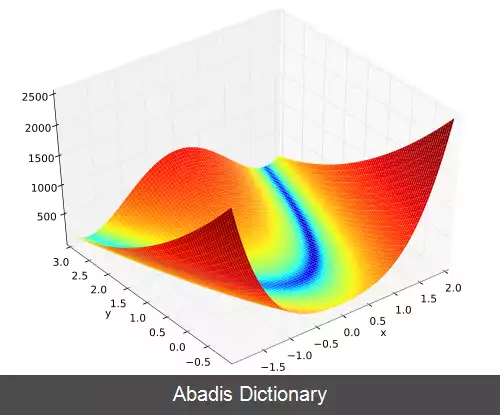
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه هدف آن پیدا کردن مینیمم و بهینه کردن تابع سهمی وار شکل شده تخت
شکل کلی تابع اینگونه تعریف شده است:
f ( x , y ) = ( a − x ) 2 + b ( y − x 2 ) 2
نقطه مینیمم بهینه ( x , y ) = ( a , a 2 ) جایی که f ( x , y ) = 0 . که معمولاً a = 1 و b = 100 .
در دو نوع معمولاً اتفاق می افتد اولی مجموع N / 2 و دومی مشکلات غیر همراه 2D Rosenbrock
این نوع دیگر که تنها تعریف شده برای هر N و راه حل های ساده قابل پیش بینی.
A بیشتر درگیر نوع است
این نوع نشان داده شده است که دقیقاً یک حداقل N = 3 ( در ( 1 , 1 , 1 ) ) و دقیقاً دو کمترین برای 4 ≤ N ≤ 7 جهانی حداقل همه آنهایی که محلی حداقل در نزدیکی ( x 1 , x 2 , … , x N ) = ( − 1 , 1 , … , 1 ) . این نتیجه به دست آمده است با تنظیم شیب تابع برابر صفر توجه است که در نتیجه معادله یک تابع منطقی x است. برای N چندجمله ای تعیین می شود و دقیقاً قضیه استورم می تواند مورد استفاده برای تعیین تعداد ریشه های واقعی در حالی که ریشه ها را می توان محدود در منطقه | x i | < 2. 4 است. [ ۴] برای بزرگتر N این روش معافیت های پایین با توجه به اندازه ضرایب درگیر است.
بسیاری از نقاط ثابت از تابع نشان یک الگوی منظم که رسم شده است؛ که این ساختار می تواند برای آن ها را بیابید.
این تابع روزن بروک می تواند کارآمد بهینه سازی شده توسط تطبیق مناسب و هماهنگ کردن سیستم بدون استفاده از هر گونه شیب اطلاعات و بدون ساختمان محلی تقریب ( در مقایسه با بسیاری از derivate - رایگان بهینه ) . شکل زیر نشان می دهد به عنوان مثال از ۲ بعدی Rosenbrock تابع بهینه سازی توسط تطبیقی هماهنگ تبار از نقطه شروع x 0 = ( − 3 , − 4 ) . این راه حل با مقدار تابع را 10 − 10 می توان پس از ۳۲۵ تابع ارزیابی است.



wiki: تابع روزن بروک
