تابع توزیع تجمعی ( به انگلیسی: Cumulative distribution function ) یا تابع توزیع انباشتی تابعی غیر صفر و هم نوای صعودی است که برد آن بازه بوده و احتمال آنکه متغیر تصادفی X دارای مقداری کوچک تر از x باشد را نشان می دهد، [ ۱] یعنی x → F X ( x ) = P ( X ≤ x ) [ ۲]
از این تعریف می توان نتیجه گرفت که:
P ( a < X ≤ b ) = F X ( b ) − F X ( a )
تابع توزیع تجمعی را می توان به صورت زیر بر اساس تابع چگالی احتمال نیز تعریف کرد
F ( x ) = ∫ − ∞ x f ( t ) d t . [ ۳]
در مورد متغیرهای تصادفی با مقادیر گسسته این تعریف به صورت زیر است:
Pr ( X = x ) = F ( x 0 ) − F ( x 0 − ) ,
که در اینجا F ( x 0 − ) به معنی حد چپ تابع F X ( x ) است وقتی که x به x 0 میل می کند[ ۱]
• تابع توزیع تجمعی برای متغیر تصادفی گسسته به این شکل تعریف می شود:
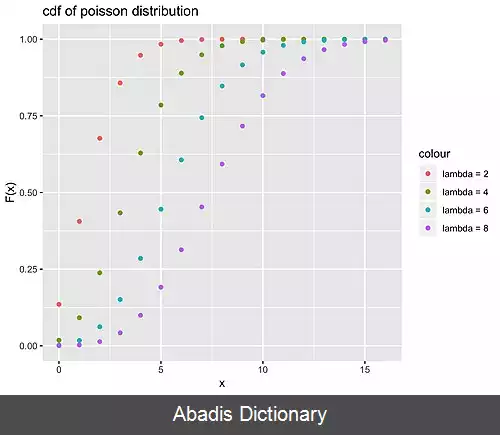
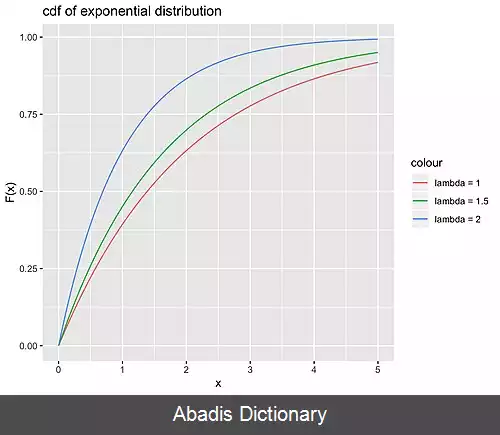
F X ( x ) = P ( X ≤ x ) = ∑ t ≤ x P ( t ) نمودار تابع توزیع تجمعی برای متغیر تصادفی گسسته تعریف تابع توزیع تجمعی برای متغیر تصادفی پیوسته به این شکل می شود : F X ( x ) = P ( X ≤ x ) = ∫ t ≤ x f ( t ) d t تمام توابع توزیع تجمعی صعودی ( ولی نه لزوماً اکیدا صعودی ) و از راست پیوسته هستند. 0 ≤ F X ( x ) ≤ 1 lim x → − ∞ F ( x ) = 0 lim x → + ∞ F ( x ) = 1 [ ۱] اگر x 1 ≤ x 2 باشد، آنگاه : F X ( x 1 ) ≤ F X ( x 2 ) P ( X > x ) = 1 − F X ( x ) P ( x 1 < x ≤ x 2 ) = F X ( x 2 ) − F X ( x 1 ) اگر M میانه داده ها باشد داریم : F X ( M ) = ∫ − ∞ M f ( x ) d x = 1 2 و این همان تعریف میانه است که نیمی از داده ها مقداری کمتر از M دارند. [ ۴]
فرض کنید X یک متغیر تصادفی پیوسته است که تابع چگالی احتمال آن به این شکل تعریف شده باشد:[ ۵]
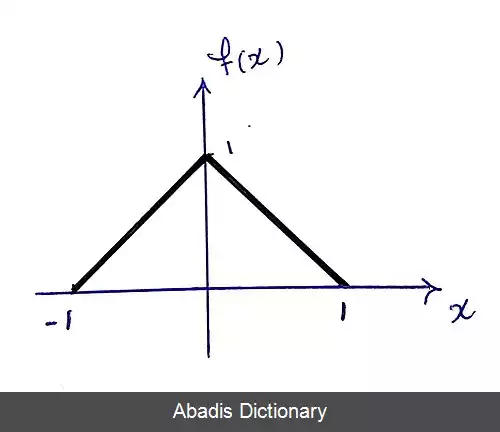
f ( x ) = { 0 x ≤ − 1 x + 1 − 1 < x ≤ 0 1 − x 0 < x < 1 0 x ≥ 1 نمودار چگالی احتمال این متغیر تصادفی به شکل زیر خواهد بود:
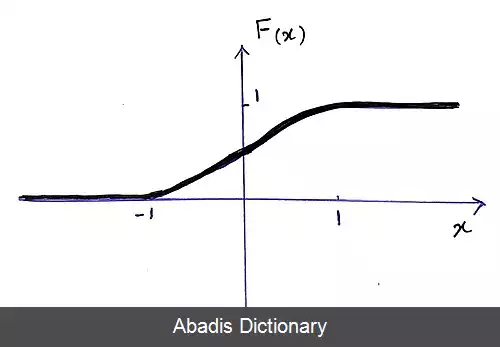
با انتگرال گیری از تابع چگالی احتمال در هر بازه تابع توزیع تجمعی آن را به دست می آوریم و خواهیم داشت: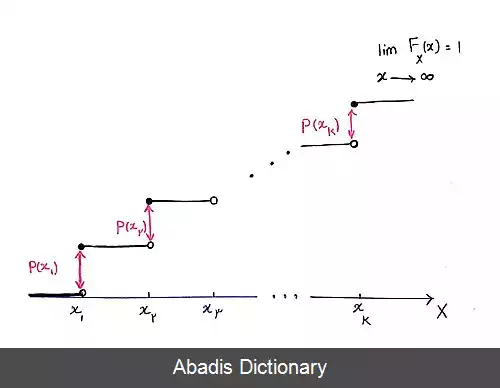
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز این تعریف می توان نتیجه گرفت که:
P ( a < X ≤ b ) = F X ( b ) − F X ( a )
تابع توزیع تجمعی را می توان به صورت زیر بر اساس تابع چگالی احتمال نیز تعریف کرد
F ( x ) = ∫ − ∞ x f ( t ) d t . [ ۳]
در مورد متغیرهای تصادفی با مقادیر گسسته این تعریف به صورت زیر است:
Pr ( X = x ) = F ( x 0 ) − F ( x 0 − ) ,
که در اینجا F ( x 0 − ) به معنی حد چپ تابع F X ( x ) است وقتی که x به x 0 میل می کند[ ۱]
• تابع توزیع تجمعی برای متغیر تصادفی گسسته به این شکل تعریف می شود:
F X ( x ) = P ( X ≤ x ) = ∑ t ≤ x P ( t ) نمودار تابع توزیع تجمعی برای متغیر تصادفی گسسته تعریف تابع توزیع تجمعی برای متغیر تصادفی پیوسته به این شکل می شود : F X ( x ) = P ( X ≤ x ) = ∫ t ≤ x f ( t ) d t تمام توابع توزیع تجمعی صعودی ( ولی نه لزوماً اکیدا صعودی ) و از راست پیوسته هستند. 0 ≤ F X ( x ) ≤ 1 lim x → − ∞ F ( x ) = 0 lim x → + ∞ F ( x ) = 1 [ ۱] اگر x 1 ≤ x 2 باشد، آنگاه : F X ( x 1 ) ≤ F X ( x 2 ) P ( X > x ) = 1 − F X ( x ) P ( x 1 < x ≤ x 2 ) = F X ( x 2 ) − F X ( x 1 ) اگر M میانه داده ها باشد داریم : F X ( M ) = ∫ − ∞ M f ( x ) d x = 1 2 و این همان تعریف میانه است که نیمی از داده ها مقداری کمتر از M دارند. [ ۴]
فرض کنید X یک متغیر تصادفی پیوسته است که تابع چگالی احتمال آن به این شکل تعریف شده باشد:[ ۵]
f ( x ) = { 0 x ≤ − 1 x + 1 − 1 < x ≤ 0 1 − x 0 < x < 1 0 x ≥ 1 نمودار چگالی احتمال این متغیر تصادفی به شکل زیر خواهد بود:
با انتگرال گیری از تابع چگالی احتمال در هر بازه تابع توزیع تجمعی آن را به دست می آوریم و خواهیم داشت:






wiki: تابع توزیع تجمعی
