در آنالیز ترکیبی، تابع بیضوی، یک تابع مرومورفیک است که در دو مسیر تناوبی است. در یک تابع متناوب، تابع فقط در یک تناوب تعریف می شود ( این تناوب پیوسته تکرار می شود ) ، اما تابع بیضوی در یک متوازی الأضلاع پایه تعریف می شود، که این متوازی الأضلاع به صورت شبکه ای تکرار می شود. چون یک تابع متناوب دوقلو نمی تواند هام دیس ( دارای دو انتهای متقارن ) باشد، بر اساس قضیهٔ لیویل باید ثابت باشد. یک تابع بیضوی باید حداقل دو قطب در متوازی الأضلاع پایه داشته باشد.
تابع بیضوی اولین بار توسط نیلس هنریک آبل به عنوان معکوس انتگرال بیضوی مطرح شد و توسط ژاکوبی گسترش یافت. از این تابع در مطالعات مربوط به محاسبهٔ طول قوس بیضی استفاده شده و به همین اساس نامگذاری شده است. توابع بیضوی ژاکوبی کاربردهای فراوانی در فیزیک یافت و خودش هم در اثبات بعضی مسائل در نظریه اعداد مقدماتی از آن استفاده کرد. کارل وایرشتراس مطالعات کامل تری راجع به این تابع انجام داد و تابع بیضوی ساده ای پیدا کرد که دیگر توابع را پوشش می داد.
یک تابع بیضوی تابعی f است که روی C تابع مرومورفیک است و برای آن دو عدد مختلط غیر صفر ω 1 و ω 2 که ω 1 ω 2 ∉ R ( به عبارت دیگر، این دو عدد غیر موازی اند ) است وجود دارد، به طوری که f ( z ) = f ( z + ω 1 ) و f ( z ) = f ( z + ω 2 ) برای هر z ∈ C .
«شبکهٔ تناوب ها» با Λ = { m ω 1 + n ω 2 ∣ m , n ∈ Z } نمایش داده می شود، در نتیجه f ( z ) = f ( z + ω ) برای هر ω ∈ Λ . دو دسته تابع بیضوی کانونی داریم:ژاکوبی و وایرشتراس. گرچه تابع بیضوی ژاکوبی قدیمی تر و مستقیماً مرتبط با کاربردهاست ولی نویسندگان جدید نظریهٔ مقدماتی را با تابع وایرشتراس دنبال می کنند چون ساده تر است. اگر یک سلول را متوازی الأضلاع پایه ای که در آن تابع چند مقداری ( چندگانه ) نباشد، تعریف کنیم، خواص زیر را خواهیم داشت: ̈# تعداد قطب ها در هر سلول محدود است.
• تعداد ریشه ها در ر سلول محدود است.
• مجموع باقیمانده ها در هر سلول صفر است.
• قضیه لیویل برای تابع بیضوی: تابع بیضوی که در یک سلول قطب نداشته باشد، ثابت است.
• تعداد صفرهای f ( z ) − c {\displaystyle f ( z ) - c} ( درجه ) برابر تعداد قطب های f ( z ) {\displaystyle f ( z ) } است.
• ساده ترین تابع بیضوی درجه ۲ است. چون یک تابع درجه اول که قطب تحویل ناپذیر و باقیمانده غیر صفر داشته باشد، غیرممکن است.
• تابع بیضوی که یک قطب درجه دو با باقیمانده صفر دارد را تابع بیضوی وایرشتراس گویند.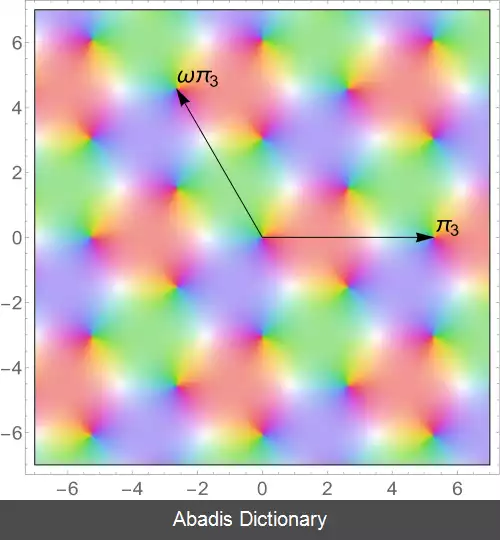
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع بیضوی اولین بار توسط نیلس هنریک آبل به عنوان معکوس انتگرال بیضوی مطرح شد و توسط ژاکوبی گسترش یافت. از این تابع در مطالعات مربوط به محاسبهٔ طول قوس بیضی استفاده شده و به همین اساس نامگذاری شده است. توابع بیضوی ژاکوبی کاربردهای فراوانی در فیزیک یافت و خودش هم در اثبات بعضی مسائل در نظریه اعداد مقدماتی از آن استفاده کرد. کارل وایرشتراس مطالعات کامل تری راجع به این تابع انجام داد و تابع بیضوی ساده ای پیدا کرد که دیگر توابع را پوشش می داد.
یک تابع بیضوی تابعی f است که روی C تابع مرومورفیک است و برای آن دو عدد مختلط غیر صفر ω 1 و ω 2 که ω 1 ω 2 ∉ R ( به عبارت دیگر، این دو عدد غیر موازی اند ) است وجود دارد، به طوری که f ( z ) = f ( z + ω 1 ) و f ( z ) = f ( z + ω 2 ) برای هر z ∈ C .
«شبکهٔ تناوب ها» با Λ = { m ω 1 + n ω 2 ∣ m , n ∈ Z } نمایش داده می شود، در نتیجه f ( z ) = f ( z + ω ) برای هر ω ∈ Λ . دو دسته تابع بیضوی کانونی داریم:ژاکوبی و وایرشتراس. گرچه تابع بیضوی ژاکوبی قدیمی تر و مستقیماً مرتبط با کاربردهاست ولی نویسندگان جدید نظریهٔ مقدماتی را با تابع وایرشتراس دنبال می کنند چون ساده تر است. اگر یک سلول را متوازی الأضلاع پایه ای که در آن تابع چند مقداری ( چندگانه ) نباشد، تعریف کنیم، خواص زیر را خواهیم داشت: ̈# تعداد قطب ها در هر سلول محدود است.
• تعداد ریشه ها در ر سلول محدود است.
• مجموع باقیمانده ها در هر سلول صفر است.
• قضیه لیویل برای تابع بیضوی: تابع بیضوی که در یک سلول قطب نداشته باشد، ثابت است.
• تعداد صفرهای f ( z ) − c {\displaystyle f ( z ) - c} ( درجه ) برابر تعداد قطب های f ( z ) {\displaystyle f ( z ) } است.
• ساده ترین تابع بیضوی درجه ۲ است. چون یک تابع درجه اول که قطب تحویل ناپذیر و باقیمانده غیر صفر داشته باشد، غیرممکن است.
• تابع بیضوی که یک قطب درجه دو با باقیمانده صفر دارد را تابع بیضوی وایرشتراس گویند.

wiki: تابع بیضوی
