در ریاضیات، تابع انتگرال لگاریتم یا انتگرال لگاریتم نام یکی از توابع ویژه است. با توجه به قضیه سیگل - والفیزز این تابع تقریب بسیار خوبی به عنوان تعداد اعداد اول کمتر مساوی با یک مقداد معین میزند که کاربرد بسیاری را در فیزیک و نظریه اعداد اول ایفا می کند.
تابع انتگرال لگاریتم را با نماد l i ( x ) نمایش می دهند و به صورت زیر تعریف می شود
l i ( x ) = ∫ 0 x d t ln t .
تابع انتگرال لگاریتم را می توان به صورت چندین سری مختلف نمایش داد. برای مثال:
که در اینجا γ ثابت اویلر نام دارد و حدوداً برابر است با γ ≈ 0. 57721 56649 01532
برای این تابع هم ارزی های مختلفی وجود دارد از جمله
l i ( x ) = O ( x ln x )
l i ( x ) ∼ x ln x ∑ k = 0 ∞ k ! ( ln x ) k
l i ( x ) x / ln x ∼ 1 + 1 ln x + 2 ( ln x ) 2 + 6 ( ln x ) 3 + ⋯
تابع آفست انتگرال لگاریتم را با نماد L i ( x ) نمایش می دهند و به صورت زیر تعریف می شود
L i ( x ) = ∫ 2 x d t ln t = l i ( x ) − l i ( 2 )
این تابع در ریاضیات گسسته و نظریه اعداد اول کاربرد قابل توجهی را دارا می باشد مثلاً ثابت شده است که :
π ( x ) ∼ Li ( x )
که در آن π ( x ) تابع شمارش اعداد اول است .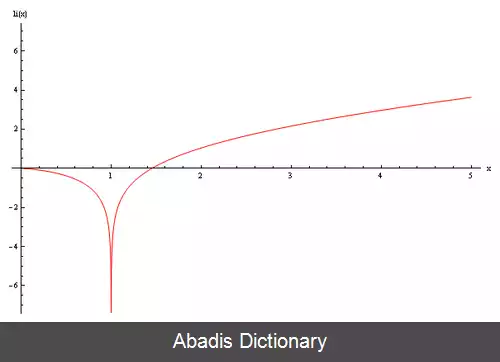
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع انتگرال لگاریتم را با نماد l i ( x ) نمایش می دهند و به صورت زیر تعریف می شود
l i ( x ) = ∫ 0 x d t ln t .
تابع انتگرال لگاریتم را می توان به صورت چندین سری مختلف نمایش داد. برای مثال:
که در اینجا γ ثابت اویلر نام دارد و حدوداً برابر است با γ ≈ 0. 57721 56649 01532
برای این تابع هم ارزی های مختلفی وجود دارد از جمله
l i ( x ) = O ( x ln x )
l i ( x ) ∼ x ln x ∑ k = 0 ∞ k ! ( ln x ) k
l i ( x ) x / ln x ∼ 1 + 1 ln x + 2 ( ln x ) 2 + 6 ( ln x ) 3 + ⋯
تابع آفست انتگرال لگاریتم را با نماد L i ( x ) نمایش می دهند و به صورت زیر تعریف می شود
L i ( x ) = ∫ 2 x d t ln t = l i ( x ) − l i ( 2 )
این تابع در ریاضیات گسسته و نظریه اعداد اول کاربرد قابل توجهی را دارا می باشد مثلاً ثابت شده است که :
π ( x ) ∼ Li ( x )
که در آن π ( x ) تابع شمارش اعداد اول است .

wiki: تابع انتگرال لگاریتم
