تابع احتمال بقا ( Survival function ) تابع توزیع احتمال بقا ( یا به بیان مهندسی reliability function ) نمایانگر احتمال بقای یک بیمار یا دوام عملکرد یک دستگاه به مدت زمان مشخص حداقل ( t ) است. این تابع به بررسی احتمال اختلال در عملکرد اجزا و سیستم ها می پردازد؛ در نتیجه، در طراحی سیستم های الکتریکی و مکانیکی و همچنین بررسی ازمایشهای پزشکی کاربرد دارد.
بنابر تعریف یاد شده، مقدار این تابع ( ( R ( t ) از رابطه زیر قابل محاسبه است :
R ( t ) = P r ( T > t ) = ∫ t ∞ f ( u ) d u = 1 − F ( t )
که در ( f ( u تابع توزیع چگالی احتمال بقای متغیر تصادفی T تا زمان t است.
• تابع reliability function یک تابع نزولی است.
• R ( 0 ) = P r ( T > 0 ) = 1 {\displaystyle R ( 0 ) =Pr ( T> 0 ) =1}
• R ( ∞ ) = 0 {\displaystyle R ( \infty ) =0}
• 0 ≤ R ( t ) ≤ 1 {\displaystyle 0\leq R ( t ) \leq 1}
در تصویر زیر چهار تابع توزیع احتمال بقا مشاهده می شود که محور x بیانگر زمان و محور y معادل احتمال بقای یک شی است.
هر یک از این نمودارهای احتمال بقای شی پس از زمان مشخص t را نشان می دهند.
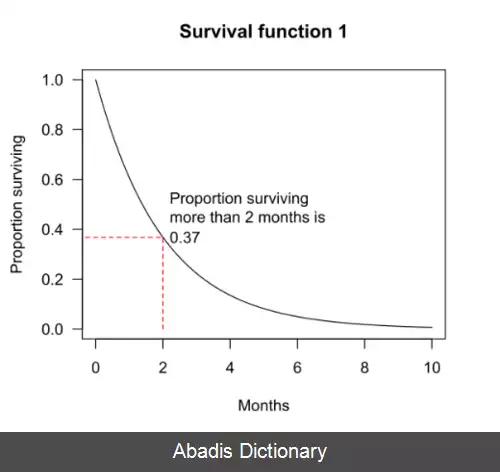
به عنوان مثال؛ در نمودار شماره یک، احتمال بقا موجود به اندازه حداقل ۲ ماه معادل ۳۷٪ است.
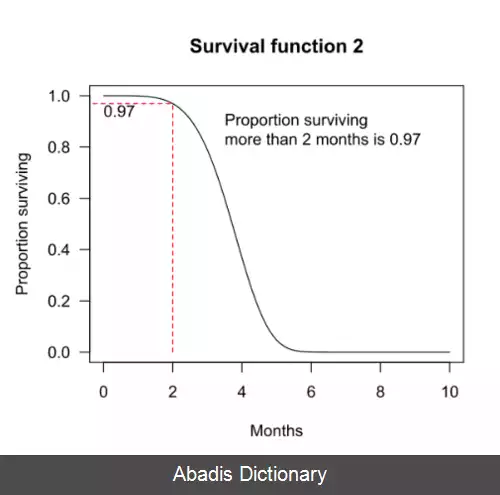
و در نمودار شماره دو، احتمال بقا برای حداقل ۲ ماه برابر ۹۷٪ است.
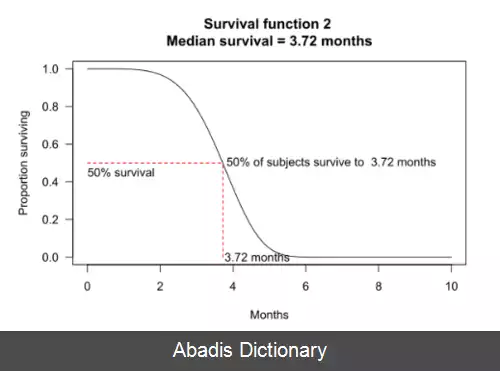
گاهی می توان میانه زمان بقا جسم را از روی نمودار تشخیص داد؛ به عنوان مثال، در نمودار شماره ۲، ۵۰٪ از اشیا حداقل ۳٫۷۲ ماه عمر کرده اند.
نمودار توزیع احتمال شکست یک رویداد تا قبل از زمان t تابع توزیع احتمال تجمعی این متغیر نامیده می شود. در واقع توزیع احتمال تجمعی بیانگر احتمال بقای یک جسم به مدت زمان کمتر از t است. در نتیجه بنابر تعریف بالا داریم:
F ( t ) = P ( T ≤ t )
که در آن، متغیر تصادفی T، زمان بقای جسم است؛ و تابع F برابر احتمال بقای جسم تا قبل از زمان t است.
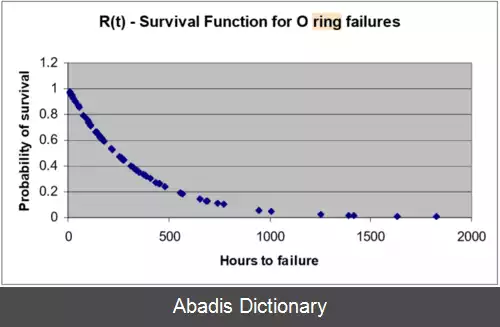
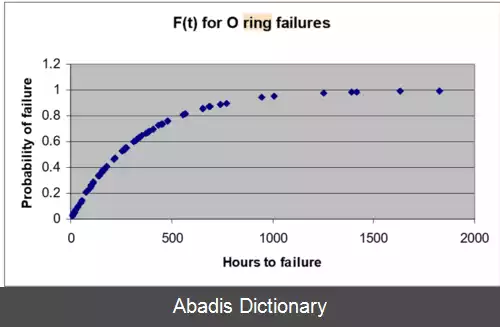
در دو نمودار زیر تابع توزیع احتمال تجمعی بقای یک O - ring تا لحظه t و تابع احتمال بقای این جسم به مدت زمان حداقل t نمایش داده شده است.
همان طور که از نمودار قابل تشخیص است؛ جمع مقادیر این دو نمودار همواره برابر مقدار ۱ است؛ چرا که مجموع احتمال بقای جسم تا زمان t و احتمال بقای آن پس از زمان t، برابر احتمال بقای این جسم از لحظه T=۰ تا بینهایت است؛ که این احتمال برابر ۱ می باشد.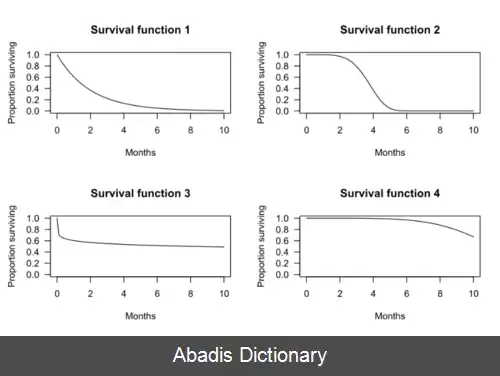
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبنابر تعریف یاد شده، مقدار این تابع ( ( R ( t ) از رابطه زیر قابل محاسبه است :
R ( t ) = P r ( T > t ) = ∫ t ∞ f ( u ) d u = 1 − F ( t )
که در ( f ( u تابع توزیع چگالی احتمال بقای متغیر تصادفی T تا زمان t است.
• تابع reliability function یک تابع نزولی است.
• R ( 0 ) = P r ( T > 0 ) = 1 {\displaystyle R ( 0 ) =Pr ( T> 0 ) =1}
• R ( ∞ ) = 0 {\displaystyle R ( \infty ) =0}
• 0 ≤ R ( t ) ≤ 1 {\displaystyle 0\leq R ( t ) \leq 1}
در تصویر زیر چهار تابع توزیع احتمال بقا مشاهده می شود که محور x بیانگر زمان و محور y معادل احتمال بقای یک شی است.
هر یک از این نمودارهای احتمال بقای شی پس از زمان مشخص t را نشان می دهند.
به عنوان مثال؛ در نمودار شماره یک، احتمال بقا موجود به اندازه حداقل ۲ ماه معادل ۳۷٪ است.
و در نمودار شماره دو، احتمال بقا برای حداقل ۲ ماه برابر ۹۷٪ است.
گاهی می توان میانه زمان بقا جسم را از روی نمودار تشخیص داد؛ به عنوان مثال، در نمودار شماره ۲، ۵۰٪ از اشیا حداقل ۳٫۷۲ ماه عمر کرده اند.
نمودار توزیع احتمال شکست یک رویداد تا قبل از زمان t تابع توزیع احتمال تجمعی این متغیر نامیده می شود. در واقع توزیع احتمال تجمعی بیانگر احتمال بقای یک جسم به مدت زمان کمتر از t است. در نتیجه بنابر تعریف بالا داریم:
F ( t ) = P ( T ≤ t )
که در آن، متغیر تصادفی T، زمان بقای جسم است؛ و تابع F برابر احتمال بقای جسم تا قبل از زمان t است.
در دو نمودار زیر تابع توزیع احتمال تجمعی بقای یک O - ring تا لحظه t و تابع احتمال بقای این جسم به مدت زمان حداقل t نمایش داده شده است.
همان طور که از نمودار قابل تشخیص است؛ جمع مقادیر این دو نمودار همواره برابر مقدار ۱ است؛ چرا که مجموع احتمال بقای جسم تا زمان t و احتمال بقای آن پس از زمان t، برابر احتمال بقای این جسم از لحظه T=۰ تا بینهایت است؛ که این احتمال برابر ۱ می باشد.






wiki: تابع احتمال بقا
