تئوری تیر تیموشنکو ( ( به انگلیسی: Timoshenko beam theory ) ) در اویل قرن بیستم توسط دانشمند و مهندس روس استفن تیموشنکو ( به انگلیسی: Stephen Timoshenko ) که اصالتی اکراینی داشت ارائه شد. [ ۱] [ ۲] این مدل با در نظر گرفتن اثر همزمان تغییرشکل برشی و ممان پیچشی، به مدلی مناسب برای شرح رفتار تیرهای کوتاه، تیرهای مرکب ساندویچی ( به انگلیسی: sandwich composite beams ) و تیرهای تحت تأثیر تحریک کننده فرکانس بالا ( در طول موج های نزدیک به ضخامت تیر ) بدل شد. فرضیات تئوری تیر تیموشنکو:
• هر صفحه به صورت صفحه باقی می ماند.
• ضخامت تیر بعد از تغییر شکل تغییر نمی کند.
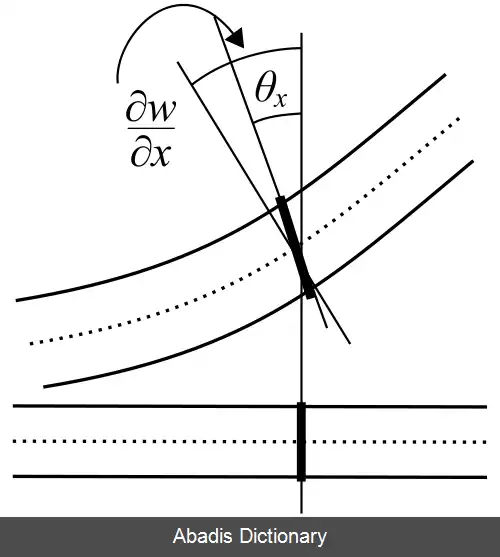
همانطور که در تصویر مشاهده می کنید فرض عمود باقی ماندن صفحات عمود بر محور خنثی که در تئوری اویلر - برنولی وجود داشت در اینجا حذف شده است. در واقع در تیر تیموشنکو، تغییرشکل های برشی خود را به صورت تغییر در زاویه این صفحات نشان می دهند. [ ۳] [ ۴]
در معادله جواب در این روش علاوه بر وجود یک ترم درجه چهار، یک مشتق جزئی درجه دوم نیز وجود دارد ( بر خلاف تئوری تیر اویلر - برنولی ) .
در حالت بارگذاری استاتیکی در تئوری تیر تیموشنکو و بدون در نظر گرفتن نیروهای محوری، فرض می شود که تغییر مکان از رابطه زیر بدست می آید:
اگر ( x , y , z ) مختصات یک نقطه بر روی تیر باشند u x , u y , u z بردارهای تغییرمکان آن نقطه در راستای دستگاه مختصات فرضی است. φ زاویه چرخش بردار عمود بر صفحه میانی تیر و w تغییرمکان این صفحه در راستای z است.
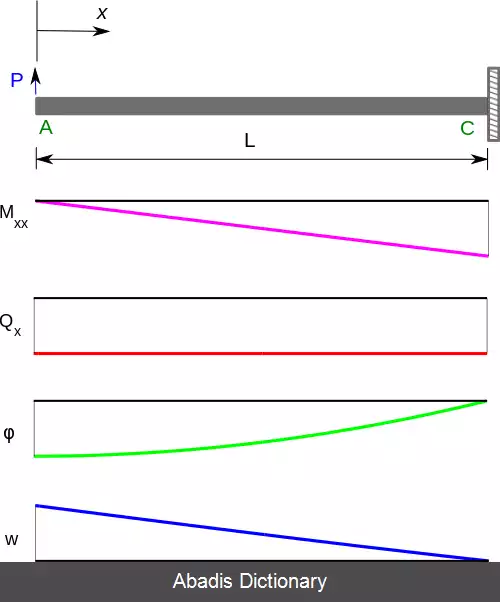
معادلات حاکم بر مسئله که از نوع معادلات دیفرانسیل معمولی هستند از این قرار خواهند بود:
تئوری تیر تیموشنکو در حالت استاتیکی و در صورتی که طرف راست معادله فوق ناچیز در نظر گرفته شود با تئوری اویلر - برنولی برابر خواهد بود. این برابری تنها با وجود شرط زیر برقرار است:
که در عبارت فوق:
• L {\displaystyle L} طول تیر
• A {\displaystyle A} سطح مقطع تیر
• E {\displaystyle E} مدول الاستیسیته تیر
• G {\displaystyle G} مدول برشی تیر
• I {\displaystyle I} گشتاور دوم سطح تیر
• و κ {\displaystyle \kappa } ضریب برش تیموشنکو است که به سطح مقطع تیر بستگی دارد. این عدد برای مقاطع مستطیلی برابر با κ = 5 / 6 {\displaystyle \kappa =5/6} است.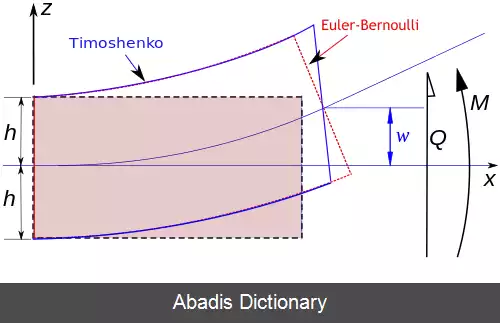
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• هر صفحه به صورت صفحه باقی می ماند.
• ضخامت تیر بعد از تغییر شکل تغییر نمی کند.
همانطور که در تصویر مشاهده می کنید فرض عمود باقی ماندن صفحات عمود بر محور خنثی که در تئوری اویلر - برنولی وجود داشت در اینجا حذف شده است. در واقع در تیر تیموشنکو، تغییرشکل های برشی خود را به صورت تغییر در زاویه این صفحات نشان می دهند. [ ۳] [ ۴]
در معادله جواب در این روش علاوه بر وجود یک ترم درجه چهار، یک مشتق جزئی درجه دوم نیز وجود دارد ( بر خلاف تئوری تیر اویلر - برنولی ) .
در حالت بارگذاری استاتیکی در تئوری تیر تیموشنکو و بدون در نظر گرفتن نیروهای محوری، فرض می شود که تغییر مکان از رابطه زیر بدست می آید:
اگر ( x , y , z ) مختصات یک نقطه بر روی تیر باشند u x , u y , u z بردارهای تغییرمکان آن نقطه در راستای دستگاه مختصات فرضی است. φ زاویه چرخش بردار عمود بر صفحه میانی تیر و w تغییرمکان این صفحه در راستای z است.
معادلات حاکم بر مسئله که از نوع معادلات دیفرانسیل معمولی هستند از این قرار خواهند بود:
تئوری تیر تیموشنکو در حالت استاتیکی و در صورتی که طرف راست معادله فوق ناچیز در نظر گرفته شود با تئوری اویلر - برنولی برابر خواهد بود. این برابری تنها با وجود شرط زیر برقرار است:
که در عبارت فوق:
• L {\displaystyle L} طول تیر
• A {\displaystyle A} سطح مقطع تیر
• E {\displaystyle E} مدول الاستیسیته تیر
• G {\displaystyle G} مدول برشی تیر
• I {\displaystyle I} گشتاور دوم سطح تیر
• و κ {\displaystyle \kappa } ضریب برش تیموشنکو است که به سطح مقطع تیر بستگی دارد. این عدد برای مقاطع مستطیلی برابر با κ = 5 / 6 {\displaystyle \kappa =5/6} است.



wiki: تئوری تیر تیموشنکو
