در آنالیز ریاضی، بیشینه ( ماکسیمم ) و کمینهٔ ( مینیمم ) یک تابع ( که به طور جمعی به آنها اکسترمم های آن تابع گویند ) به ترتیب، به بزرگترین مقدار و کوچکترین مقدار تابع ( در صورت وجود ) ، یا در یک بازهٔ خاص ( اکسترمم نسبی ) و یا در کلّ دامنه ( اکسترمم مطلق ) گفته می شود. [ ۱]
فرما، یکی از اوّلین کسانی بود که روشی کلّی برای پیدا کردن اکسترمم ها پیشنهاد کردند.
نقطهٔ بیشینهٔ مطلق a ( که با m a x ( f ( x ) ) نشان می دهند ) در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( a ) ⩾ f ( x ) ; ∀ x ∈ D .
به شکل مشابه، نقطهٔ کمینهٔ مطلق b ( که با m i n ( f ( x ) ) نشان می دهند ) در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( b ) ⩽ f ( x ) ; ∀ x ∈ D .
در بیشتر اوقات، صفت «مطلق» برای اکسترمم مطلق ذکر نمی شود.
نقطهٔ بیشینهٔ نسبی a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , d ( a , x ) < ε ) f ( a ) ⩾ f ( x ) .
تابع فاصله d در فضای متریک برای اعداد حقیقی به صورت d ( x , y ) = | x − y | تعریف می شود.
به شکل مشابه، نقطهٔ کمینهٔ نسبی b در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , d ( b , x ) < ε ) f ( b ) ⩽ f ( x ) .
مفهوم اکید را می توان برای هر دو اکسترمم مطلق و نسبی تعریف کرد. به عنوان مثال:
نقطهٔ بیشینهٔ مطلق اکید a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( a ) > f ( x ) ; ∀ x ∈ D , x ≠ a .
نقطهٔ بیشینهٔ نسبی اکید a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , x ≠ a , d ( a , x ) < ε ) f ( a ) > f ( x ) .
یافتن اکسترمم ها هدف بهینه سازی است.
• اگر تابع f {\displaystyle f} در بازهٔ {\displaystyle } پیوسته باشد، آن گاه f {\displaystyle f} روی {\displaystyle } دارای حدّاقل یک مقدار بیشینهٔ مطلق و یک مقدار کمینهٔ مطلق است.
همان طور که از صورت قضیهٔ اکسترمم ملاحظه می شود شرط کافی برای وجود اکسترمم مطلق، پیوسته بودن تابع در فاصلهٔ است؛ ولی با این وجود، این شرط لازم نیست، چون تابعی می توان نشان داد که در فاصله ای پیوسته نباشد ولی دارای بیشینه و کمینهٔ مطلق باشد. به عبارت دیگر نمی توان گفت که چون تابعی در بازه ای ناپیوسته است، بیشینه و کمینهٔ مطلق ندارد. اما اگر تابعی در بازهٔ بسته ای پیوسته باشد، آن گاه حتماً دارای بیشینه و کمینهٔ مطلق هست. [ ۲]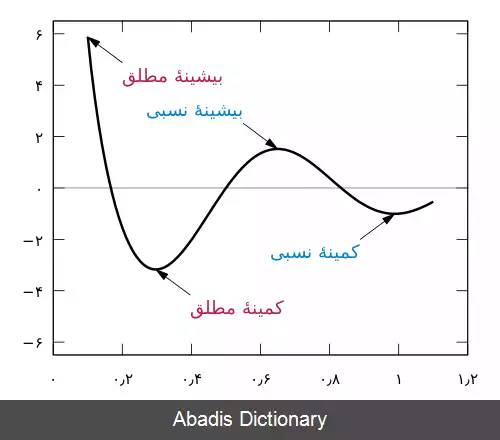
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرما، یکی از اوّلین کسانی بود که روشی کلّی برای پیدا کردن اکسترمم ها پیشنهاد کردند.
نقطهٔ بیشینهٔ مطلق a ( که با m a x ( f ( x ) ) نشان می دهند ) در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( a ) ⩾ f ( x ) ; ∀ x ∈ D .
به شکل مشابه، نقطهٔ کمینهٔ مطلق b ( که با m i n ( f ( x ) ) نشان می دهند ) در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( b ) ⩽ f ( x ) ; ∀ x ∈ D .
در بیشتر اوقات، صفت «مطلق» برای اکسترمم مطلق ذکر نمی شود.
نقطهٔ بیشینهٔ نسبی a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , d ( a , x ) < ε ) f ( a ) ⩾ f ( x ) .
تابع فاصله d در فضای متریک برای اعداد حقیقی به صورت d ( x , y ) = | x − y | تعریف می شود.
به شکل مشابه، نقطهٔ کمینهٔ نسبی b در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , d ( b , x ) < ε ) f ( b ) ⩽ f ( x ) .
مفهوم اکید را می توان برای هر دو اکسترمم مطلق و نسبی تعریف کرد. به عنوان مثال:
نقطهٔ بیشینهٔ مطلق اکید a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که f ( a ) > f ( x ) ; ∀ x ∈ D , x ≠ a .
نقطهٔ بیشینهٔ نسبی اکید a در یک تابع حقیقی f با دامنهٔ D ، نقطه ای است که ∃ ε ∈ R ∗ + : ( ∀ x ∈ D , x ≠ a , d ( a , x ) < ε ) f ( a ) > f ( x ) .
یافتن اکسترمم ها هدف بهینه سازی است.
• اگر تابع f {\displaystyle f} در بازهٔ {\displaystyle } پیوسته باشد، آن گاه f {\displaystyle f} روی {\displaystyle } دارای حدّاقل یک مقدار بیشینهٔ مطلق و یک مقدار کمینهٔ مطلق است.
همان طور که از صورت قضیهٔ اکسترمم ملاحظه می شود شرط کافی برای وجود اکسترمم مطلق، پیوسته بودن تابع در فاصلهٔ است؛ ولی با این وجود، این شرط لازم نیست، چون تابعی می توان نشان داد که در فاصله ای پیوسته نباشد ولی دارای بیشینه و کمینهٔ مطلق باشد. به عبارت دیگر نمی توان گفت که چون تابعی در بازه ای ناپیوسته است، بیشینه و کمینهٔ مطلق ندارد. اما اگر تابعی در بازهٔ بسته ای پیوسته باشد، آن گاه حتماً دارای بیشینه و کمینهٔ مطلق هست. [ ۲]

wiki: بیشینه و کمینه
