بهینه سازی ریاضی یا برنامه ریزی ریاضی در ریاضیات، اقتصاد، مدیریت به برگزیدن بهترین عضو از یک مجموعه از اعضای دست یافتنی اشاره می کند. در ساده ترین شکل تلاش می شود که با گزینش نظام مند داده ها از یک مجموعه قابل دستیابی و محاسبه مقدار یک تابع حقیقی مقدار بیشینه و کمینه آن به دست آید. در قلمرو مدیریت اصولاً دو فرض وجود دارد:
• نبود محدودیت در منابع
• وجود محدودیت در منابع
که اگر فرض نخست را بپذیریم می توان از روشهایی چون گرفتن مشتق اول و دوم مقدار بهینه را برآورد کرد و چنانچه فرض دوم پذیرفته شود بسته به نوع مسائل سازمانی واقتصادی می توان مدلهایی را چون:مدل خطی، عدد صحیح، آرمانی، غیر خطی، ضریب لاگرانژ، قطعی یا احتمالی و غیره طراحی کرد و با بهره گیری از روش های موجود به سوی نقطه بهینه حرکت کرد.
روش های تحلیلی بیشتر به دنبال حل دقیق مسائل هستند. از این رو شامل مشتق گیری و یافتن پاسخ بهینه اند. [ ۱] فایده اصلی این نوع از الگوریتم های بهینه سازی تضمین جواب بهینه است، اما استفاده از آنها در مسائل با پیچیدگی بالا یا مسائل بزرگ یا دارای تابع گسسته دشوار است. [ ۲]
روش های فراابتکاری یا فرااکتشافی برای حل مسائل بزرگتر و با توابع بدرفتار مناسب ترند. اگرچه این روش ها نمی توانند رسیدن به جواب بهینه را تضمین کنند. الگوریتم ژنتیک و تصعید شبیه سازی شده مثال هایی از این الگوریتم ها هستند. [ ۳] [ ۲]
الگوریتم هایی مانند الگوریتم پنگوئن امپراتور ( تک هدفه یا چند هدفه ) برای حل مسائل پیچیده همچون بهره برداری از مخازن سد کارآمد هستند. [ ۴]
در بهینه سازی هدفمان حفظ کردن فرمول یا رابطه ای نیست. تنها از دانش قبلی خود استفاده می کنیم. به دنبال بیشترین یا کمترین مقدار برای یک کمیت هستیم.
• گام اول، یافتن تابع تغییرات کمیتی است که با آن سر و کار داریم. در این گام باید نسبت به تعیین دامنهٔ تابع دقت کنیم.
• گام دوم، پیدا کردن نقاط بحرانی تابعی است که در گام اول یافتیم.
• گام سوم، پیدا کردن اکسترمم تابع است. بسته به خواستهٔ مسئله، گاهی این اکسترمم ماکزیمم است و گاهی مینیمم.
در علم اقتصاد و علم مدیریت برنامه ریزی ریاضی کاربرد بسیاری دارد و زیر مجموعه ای از فنون بهینه سازی و حل مسائل گوناگون اقتصادی و مدیریت به بهترین شکل باتوجه به محدودیت های مسئله اعم از منابع، زمان، مقدار و . . . با اعمال قیدها برای رسیدن به بیشترین کارایی که میتواند بیشترین سود، بیشترین تولید، کمترین هزینه، بیشترین ظرفیت، کوتاه ترین مسیر، کمترین زمان، سریع ترین زمان، کمترین ریسک و. . . با استفاده بهینه از منابع به بهترین شکل باشد.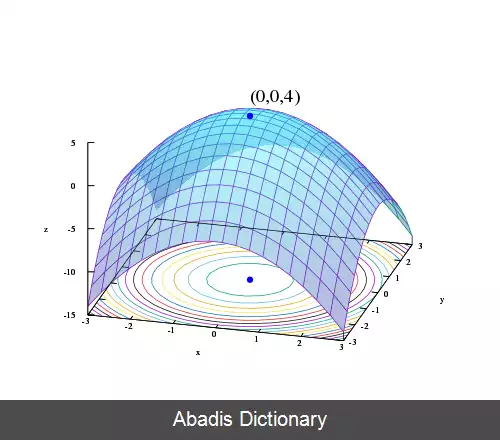

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• نبود محدودیت در منابع
• وجود محدودیت در منابع
که اگر فرض نخست را بپذیریم می توان از روشهایی چون گرفتن مشتق اول و دوم مقدار بهینه را برآورد کرد و چنانچه فرض دوم پذیرفته شود بسته به نوع مسائل سازمانی واقتصادی می توان مدلهایی را چون:مدل خطی، عدد صحیح، آرمانی، غیر خطی، ضریب لاگرانژ، قطعی یا احتمالی و غیره طراحی کرد و با بهره گیری از روش های موجود به سوی نقطه بهینه حرکت کرد.
روش های تحلیلی بیشتر به دنبال حل دقیق مسائل هستند. از این رو شامل مشتق گیری و یافتن پاسخ بهینه اند. [ ۱] فایده اصلی این نوع از الگوریتم های بهینه سازی تضمین جواب بهینه است، اما استفاده از آنها در مسائل با پیچیدگی بالا یا مسائل بزرگ یا دارای تابع گسسته دشوار است. [ ۲]
روش های فراابتکاری یا فرااکتشافی برای حل مسائل بزرگتر و با توابع بدرفتار مناسب ترند. اگرچه این روش ها نمی توانند رسیدن به جواب بهینه را تضمین کنند. الگوریتم ژنتیک و تصعید شبیه سازی شده مثال هایی از این الگوریتم ها هستند. [ ۳] [ ۲]
الگوریتم هایی مانند الگوریتم پنگوئن امپراتور ( تک هدفه یا چند هدفه ) برای حل مسائل پیچیده همچون بهره برداری از مخازن سد کارآمد هستند. [ ۴]
در بهینه سازی هدفمان حفظ کردن فرمول یا رابطه ای نیست. تنها از دانش قبلی خود استفاده می کنیم. به دنبال بیشترین یا کمترین مقدار برای یک کمیت هستیم.
• گام اول، یافتن تابع تغییرات کمیتی است که با آن سر و کار داریم. در این گام باید نسبت به تعیین دامنهٔ تابع دقت کنیم.
• گام دوم، پیدا کردن نقاط بحرانی تابعی است که در گام اول یافتیم.
• گام سوم، پیدا کردن اکسترمم تابع است. بسته به خواستهٔ مسئله، گاهی این اکسترمم ماکزیمم است و گاهی مینیمم.
در علم اقتصاد و علم مدیریت برنامه ریزی ریاضی کاربرد بسیاری دارد و زیر مجموعه ای از فنون بهینه سازی و حل مسائل گوناگون اقتصادی و مدیریت به بهترین شکل باتوجه به محدودیت های مسئله اعم از منابع، زمان، مقدار و . . . با اعمال قیدها برای رسیدن به بیشترین کارایی که میتواند بیشترین سود، بیشترین تولید، کمترین هزینه، بیشترین ظرفیت، کوتاه ترین مسیر، کمترین زمان، سریع ترین زمان، کمترین ریسک و. . . با استفاده بهینه از منابع به بهترین شکل باشد.



wiki: بهینه سازی
