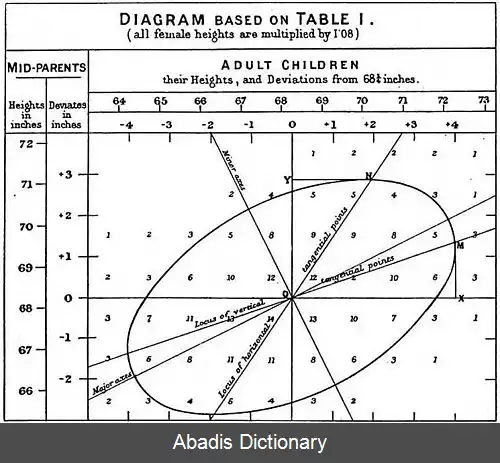
در علم آمار، برگشت به میانگین ( که واژهٔ برگشت از عبارت Regression ترجمه شده است ) به پدیده ای گفته می شود که اگر یک نمونه از متغیری تصادفی، مقداری حدی داشته باشد، نمونه گیری بعدی از همان متغیر تصادفی احتمالاً به میانگین نزدیک تر است. [ ۱] [ ۲] [ ۳] علاوه بر این، زمانی که تعداد زیادی نمونه گیری از متغیر تصادفی خاصی انجام و حدی ترین نمونه ها عمداً جدا شده باشند، ( در بسیاری از موارد ) نمونه گیریِ دوباره از این متغییرهای تفکیک شده منجر به نتایجی می شود که به میانگین اولیه تمامی متغییرها نزدیک ترند و نتایج حدی کمتری دارند.
از نظر ریاضی، شدت «برگشت» به این بستگی دارد که همهٔ متغیرهای تصادفی از یک توزیع برداشت شده باشند یا توزیع هر یک از متغییرهای تصادفی تفاوت های اساسی واقعی داشته باشد. در حالت اول، اثر «برگشت» از نظر آماری احتمال وقوع دارد، اما در مورد دوم، ممکن است احتمالی بسیار کمتر داشته باشد یا اصلاً رخ ندهد.
بنابراین، لحاظ پدیدهٔ برگشت به میانگین برای طراحی هر آزمایش علمی، تحلیل داده یا آزمونی که در آن به عمد «حدی ترین» رویدادها انتخاب می شوند مفید است. بر این اساس برای اجتناب از جمع بندی های شتاب زده در مورد این رویدادها شاید بررسی های بیشتری لازم باشد چرا که ممکن است این نمونه ها در واقع رویدادهایی حدی باشند یا به دلیل پارازیت آماری، گزینشی کاملاً بی معنی انجام شده یا ترکیبی از این دو حالت صادق باشد. [ ۴]
دانش آموزان کلاسی را در نظر بگیرید که در آزمونی با ۱۰۰ سؤال دو گزینه ای صحیح/غلط شرکت می کنند. با فرض اینکه همه دانش آموزان تصادفی پاسخ سؤال ها را انتخاب کنند، نمرهٔ هر دانش آموز مصداق حالت خاصی از مجموعهٔ متغیرهای تصادفی مستقل با توزیع یکسان، و میانگین مورد انتظار ۵۰ خواهد بود. طبیعی است که نمرهٔ برخی از دانش آموزان به طور شانسی تا حد قابل توجهی بیشتر از ۵۰ و نمرهٔ برخی دیگر به طور قابل ملاحظه ای کمتر از ۵۰ باشد. اگر فردی ۱۰ درصد از دانش آموزانی را که بیشترین امتیاز را کسب کرده اند انتخاب و آزمون دیگری برگزار کند که در آن آزمون دانش آموزان منتخب دوباره به طور تصادفی به همهٔ سؤال ها پاسخ دهند، انتظار می رود میانگین نمره های کسب شده جدید باز نزدیک به ۵۰ باشد؛ بنابراین، میانگین این دانش آموزان بار دیگر به میانگین تمام دانش آموزانی که در آزمون اصلی شرکت کرده بودند «برمی گردد». مهم نیست که هر دانش آموز در آزمون اصلی چه نمره ای گرفته باشد، بهترین پیش بینی نمرهٔ هر دانش آموز در آزمون دوم، ۵۰ است.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز نظر ریاضی، شدت «برگشت» به این بستگی دارد که همهٔ متغیرهای تصادفی از یک توزیع برداشت شده باشند یا توزیع هر یک از متغییرهای تصادفی تفاوت های اساسی واقعی داشته باشد. در حالت اول، اثر «برگشت» از نظر آماری احتمال وقوع دارد، اما در مورد دوم، ممکن است احتمالی بسیار کمتر داشته باشد یا اصلاً رخ ندهد.
بنابراین، لحاظ پدیدهٔ برگشت به میانگین برای طراحی هر آزمایش علمی، تحلیل داده یا آزمونی که در آن به عمد «حدی ترین» رویدادها انتخاب می شوند مفید است. بر این اساس برای اجتناب از جمع بندی های شتاب زده در مورد این رویدادها شاید بررسی های بیشتری لازم باشد چرا که ممکن است این نمونه ها در واقع رویدادهایی حدی باشند یا به دلیل پارازیت آماری، گزینشی کاملاً بی معنی انجام شده یا ترکیبی از این دو حالت صادق باشد. [ ۴]
دانش آموزان کلاسی را در نظر بگیرید که در آزمونی با ۱۰۰ سؤال دو گزینه ای صحیح/غلط شرکت می کنند. با فرض اینکه همه دانش آموزان تصادفی پاسخ سؤال ها را انتخاب کنند، نمرهٔ هر دانش آموز مصداق حالت خاصی از مجموعهٔ متغیرهای تصادفی مستقل با توزیع یکسان، و میانگین مورد انتظار ۵۰ خواهد بود. طبیعی است که نمرهٔ برخی از دانش آموزان به طور شانسی تا حد قابل توجهی بیشتر از ۵۰ و نمرهٔ برخی دیگر به طور قابل ملاحظه ای کمتر از ۵۰ باشد. اگر فردی ۱۰ درصد از دانش آموزانی را که بیشترین امتیاز را کسب کرده اند انتخاب و آزمون دیگری برگزار کند که در آن آزمون دانش آموزان منتخب دوباره به طور تصادفی به همهٔ سؤال ها پاسخ دهند، انتظار می رود میانگین نمره های کسب شده جدید باز نزدیک به ۵۰ باشد؛ بنابراین، میانگین این دانش آموزان بار دیگر به میانگین تمام دانش آموزانی که در آزمون اصلی شرکت کرده بودند «برمی گردد». مهم نیست که هر دانش آموز در آزمون اصلی چه نمره ای گرفته باشد، بهترین پیش بینی نمرهٔ هر دانش آموز در آزمون دوم، ۵۰ است.


wiki: برگشت به میانگین
