برش کمینه یکی از پرسمان های کلیدی در زمینهٔ بهینه سازی شبکه است. برش در اینجا برداشتن شماری از یال های گرافی همبند است به گونه ای که گراف را به دو بخش ناهمبند بِبُرد. اگر برداشتن هر یال هزینه ای داشته باشد، برش کمینه به دنبال یافتن زیرمجموعه ای از یال هاست که برداشتن این یال ها کم ترین هزینه را در پی داشته باشد.
اگر گرافی را با G ( V , E ) نمایش دهیم؛ گره ها و E یال های گراف را نشان می دهند. یک یال را به دو روش می نمایانیم. دوتایی x y یالی را نمایش می دهد که x ∈ V و y ∈ V گره های دو سر یال هستند. هم چنین e i ∈ E یال i ام را نشان می دهد. برای یافتن برش کمینه، خوارزمیک ( الگوریتم ) زیر را به کار می بریم:
• ملاحظه 2. 1: اندازه دست کم برابر اندازهٔ برش در G {\displaystyle G\!} می باشد . چون هر برشی در ، برش هم ارزی در G {\displaystyle G\!} دارد.
• ملاحظه 2. 2: اگر e 1 , . . . , e n − 2 {\displaystyle e_{1}, . . . , e_{n - 2}\!} ، دنباله ای از یال ها در G {\displaystyle G\!} باشد و G / e 1 , . . . , e n − 2 {\displaystyle G/{e_{1}, . . . , e_{n - 2}}\!} دربردارندهٔ یک یا چند یال باشد، این چند یال، هم ارز برش کمینه در G {\displaystyle G\!} می باشند.
• لم 2. 3: اگر گراف G {\displaystyle G\!} با شمار گره های ، دارای برش کمینه با اندازهٔ k {\displaystyle k\!} باشد، آنگاه داریم | E ( G ) | ≥ k n / 2 {\displaystyle \left\vert E ( G ) \right\vert \geq kn/2\!} .
• لم 2. 4: اگر به صورت تصادفی، یال e {\displaystyle e\!} را از گراف G {\displaystyle G\!} برداریم، با احتمال 2 / n {\displaystyle 2/n\!} ، این یال در برش کمینه است.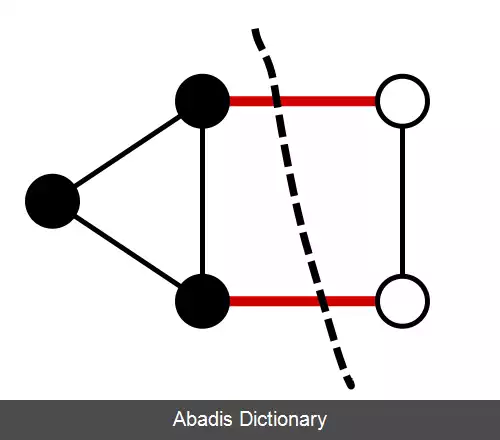
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر گرافی را با G ( V , E ) نمایش دهیم؛ گره ها و E یال های گراف را نشان می دهند. یک یال را به دو روش می نمایانیم. دوتایی x y یالی را نمایش می دهد که x ∈ V و y ∈ V گره های دو سر یال هستند. هم چنین e i ∈ E یال i ام را نشان می دهد. برای یافتن برش کمینه، خوارزمیک ( الگوریتم ) زیر را به کار می بریم:
• ملاحظه 2. 1: اندازه دست کم برابر اندازهٔ برش در G {\displaystyle G\!} می باشد . چون هر برشی در ، برش هم ارزی در G {\displaystyle G\!} دارد.
• ملاحظه 2. 2: اگر e 1 , . . . , e n − 2 {\displaystyle e_{1}, . . . , e_{n - 2}\!} ، دنباله ای از یال ها در G {\displaystyle G\!} باشد و G / e 1 , . . . , e n − 2 {\displaystyle G/{e_{1}, . . . , e_{n - 2}}\!} دربردارندهٔ یک یا چند یال باشد، این چند یال، هم ارز برش کمینه در G {\displaystyle G\!} می باشند.
• لم 2. 3: اگر گراف G {\displaystyle G\!} با شمار گره های ، دارای برش کمینه با اندازهٔ k {\displaystyle k\!} باشد، آنگاه داریم | E ( G ) | ≥ k n / 2 {\displaystyle \left\vert E ( G ) \right\vert \geq kn/2\!} .
• لم 2. 4: اگر به صورت تصادفی، یال e {\displaystyle e\!} را از گراف G {\displaystyle G\!} برداریم، با احتمال 2 / n {\displaystyle 2/n\!} ، این یال در برش کمینه است.

wiki: برش کمینه
