برج هانویْ ( در بعضی منابع «برج های هانویْ» ) ( به انگلیسی: Tower of Hanoi ) از سه میله و تعدادی دیسک در اندازه های متفاوت تشکیل شده است که می توان آن ها را بر میله ها جای داد. [ ۱] [ ۲]
در محوطه معبدی در آسیای دور سه میله الماسی قرار داشت که یکی از آن ها حاوی تعدادی قرص طلایی بود. کاهنان معبد در تلاش بودند تا قرص های طلایی را از آن میله به یکی دیگر از میله ها تحت شرایطی انتقال دهند، و باور داشتند که با تمام شدن انتقال قرص ها عمر جهان نیز به پایان خواهد رسید! میله اولیه ۶۴ قرص داشت، که بر روی هم به طور نزولی بر اساس اندازه شان چیده شده بودند. [ ۳]
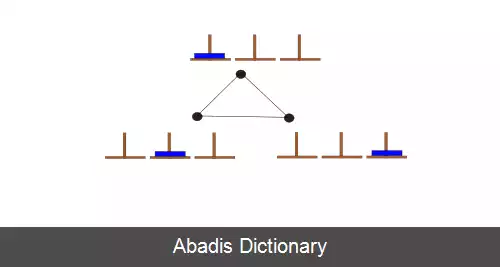
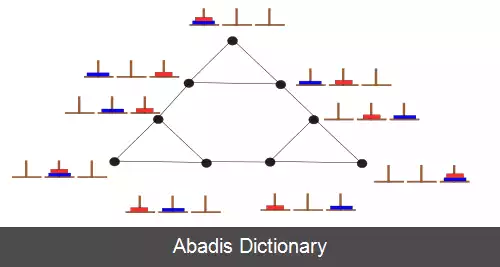
همانند شکل سه میله داریم. یکی از میله ها میله مبدأ ( A ) ، دیگری میله کمکی ( B ) و دیگری میله مقصد ( C ) است. هدف انتقال تمام دیسک ها از میله مبدأ به میله مقصد با رعایت شرایط زیر است:
در هر زمان فقط یک دیسک را می توان جابجا نمود. نباید در هیچ زمانی دیسکی بر روی دیسک با اندازه کوچکتر قرار بگیرد.
هدف ما ارائه الگوریتمی است که کمترین توالی حرکت ها را برای انتقال دیسک ها به ما بدهد؛ مثلاً اگر n=۲ باشد، توالی حرکت به صورت زیر است:
• دیسک ۱ را به میله B منتقل می کنیم.
• دیسک ۲ را به میله C منتقل می کنیم.
• دیسک ۱ را به میله C منتقل می کنیم. [ ۴]
توجه داشته باشید که بر اساس قانون اول نمی توان به غیر از بالاترین دیسک هر میله، به دیسک دیگری از آن دسترسی پیدا کرد.
حال سؤال این است که آیا این مسئله به کمک تکنیک بازگشت قابل حل است؟ اصولاً چه مسائلی را می توان بازگشتی حل نمود؟
برای اینکه مسئله ای بتواند با روش بازگشتی حل شود باید یک ویژگی اساسی داشته باشد. مسئله اصلی ( مسئله ای که به ما داده می شود ) قابل خرد شدن به زیر مسئله هایی از همان نوع مسئله اصلی باشد، به شرطی که اندازه زیر مسئله های ایجاد شده کمتر باشد. آنگاه می توان امیدوار بود که آن را به طور بازگشتی حل کرد! این ویژگی در مورد مسئله برج هانوی صدق می کند. ایده اصلی این است که توجهمان را به جای حرکت بالاترین دیسک، روی پایین ترین دیسک میله متمرکز کرده، و مراحل زیر را طی می کنیم:
n - ۱ دیسک بالایی را با شرایط ذکر شده و به کمک میله C به میله B منتقل می کنیم. بزرگترین دیسک را از میله مبدأ به میله مقصد حرکت می دهیم. n - ۱ دیسک را که هم اکنون در میله B هستند با شرایط داده شده به میله مقصد انتقال می دهیم. می بینیم که توانستیم عملیات جابجا کردن n دیسک را به دو عملیات مشابه ولی با اندازه کمتر و یک عملیات ساده تقسیم کنیم. واضح است که جابجا کردن n - ۱ قرص راحتتر از جابجا نمودن n قرص است. [ ۵]


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر محوطه معبدی در آسیای دور سه میله الماسی قرار داشت که یکی از آن ها حاوی تعدادی قرص طلایی بود. کاهنان معبد در تلاش بودند تا قرص های طلایی را از آن میله به یکی دیگر از میله ها تحت شرایطی انتقال دهند، و باور داشتند که با تمام شدن انتقال قرص ها عمر جهان نیز به پایان خواهد رسید! میله اولیه ۶۴ قرص داشت، که بر روی هم به طور نزولی بر اساس اندازه شان چیده شده بودند. [ ۳]
همانند شکل سه میله داریم. یکی از میله ها میله مبدأ ( A ) ، دیگری میله کمکی ( B ) و دیگری میله مقصد ( C ) است. هدف انتقال تمام دیسک ها از میله مبدأ به میله مقصد با رعایت شرایط زیر است:
در هر زمان فقط یک دیسک را می توان جابجا نمود. نباید در هیچ زمانی دیسکی بر روی دیسک با اندازه کوچکتر قرار بگیرد.
هدف ما ارائه الگوریتمی است که کمترین توالی حرکت ها را برای انتقال دیسک ها به ما بدهد؛ مثلاً اگر n=۲ باشد، توالی حرکت به صورت زیر است:
• دیسک ۱ را به میله B منتقل می کنیم.
• دیسک ۲ را به میله C منتقل می کنیم.
• دیسک ۱ را به میله C منتقل می کنیم. [ ۴]
توجه داشته باشید که بر اساس قانون اول نمی توان به غیر از بالاترین دیسک هر میله، به دیسک دیگری از آن دسترسی پیدا کرد.
حال سؤال این است که آیا این مسئله به کمک تکنیک بازگشت قابل حل است؟ اصولاً چه مسائلی را می توان بازگشتی حل نمود؟
برای اینکه مسئله ای بتواند با روش بازگشتی حل شود باید یک ویژگی اساسی داشته باشد. مسئله اصلی ( مسئله ای که به ما داده می شود ) قابل خرد شدن به زیر مسئله هایی از همان نوع مسئله اصلی باشد، به شرطی که اندازه زیر مسئله های ایجاد شده کمتر باشد. آنگاه می توان امیدوار بود که آن را به طور بازگشتی حل کرد! این ویژگی در مورد مسئله برج هانوی صدق می کند. ایده اصلی این است که توجهمان را به جای حرکت بالاترین دیسک، روی پایین ترین دیسک میله متمرکز کرده، و مراحل زیر را طی می کنیم:
n - ۱ دیسک بالایی را با شرایط ذکر شده و به کمک میله C به میله B منتقل می کنیم. بزرگترین دیسک را از میله مبدأ به میله مقصد حرکت می دهیم. n - ۱ دیسک را که هم اکنون در میله B هستند با شرایط داده شده به میله مقصد انتقال می دهیم. می بینیم که توانستیم عملیات جابجا کردن n دیسک را به دو عملیات مشابه ولی با اندازه کمتر و یک عملیات ساده تقسیم کنیم. واضح است که جابجا کردن n - ۱ قرص راحتتر از جابجا نمودن n قرص است. [ ۵]





wiki: برج هانوی
