برآوردگر بیشینه گر احتمال پسین. در آمار، برآوردگر بیشینه گر احتمال پسین ( به انگلیسی: Maximum a posteriori estimation ) یک پارامتر، مد توزیع احتمال پسین آن پارامتر است. به بیان ریاضی، اگر داده X بر اساس توزیع f ( X | θ ) با پارامتر θ توزیع شده باشند و g ( θ ) و f ( X | θ ) به ترتیب احتمال پیشین پارامتر و درستنمایی داده را نشان دهند، برآوردگر بیشینه گر احتمال پسین برابر خواهد بود با:
برآوردگر بیشینه گر احتمال پسین ارتباط نزدیکی با برآورد درستنمایی بیشینه دارد، با این تفاوت که برای پارامتر مورد تخمین احتمال پیشین را هم در نظر می گیرد. در نتیجه، می توان برآوردگر بیشینه گر احتمال پسین را همان برآورد درست نمایی بیشینه دانست به همراه یک تنظیم گر.
فرض کنید میخواهیم پارامتر جمعیت مشاهده نشده ی θ را بر اساس مشاهدات x تخمین بزنیم. فرض کنید f توزیع نمونه گیری x باشد، پس احتمال x وقتی که پارامتر جمعیت θ باشد، f ( x | θ ) است. تابع زیر به تابع درست نمایی معروف است:
θ ↦ f ( x | θ )
و تخمین زیر، برآورد حداکثر درست نمایی است:
θ ^ M L E ( x ) = a r g m a x θ f ( x ∣ θ )
حال فرض کنید توزیع پیشین g روی θ وجود داشته باشد. این کار به ما اجازه می دهد تا با θ به عنوان یک متغیر تصادفی رفتار کنیم. محاسبه ی توزیع پسین θ با استفاده از قانون بیز به صورت زیر است:
θ ↦ f ( θ ∣ x ) = f ( x ∣ θ ) g ( θ ) ∫ Θ f ( x ∣ ϑ ) g ( ϑ ) d ϑ
g تابع چگالی θ و Θ دامنه ی g است.
روش برآوردگر بیشینه گر احتمال پسین به صورت زیر است:
θ ^ M A P ( x ) = a r g m a x θ f ( θ ∣ x ) = a r g m a x θ f ( x ∣ θ ) g ( θ ) ∫ Θ f ( x ∣ ϑ ) g ( ϑ ) d ϑ = a r g m a x θ f ( x ∣ θ ) g ( θ ) .
مخرج کسر بالا همواره مثبت است و نیز وابسته به θ نیست، در نتیجه نقشی در بهینه سازی تابع ندارد. وقتی g تابعی ثابت باشد آن گاه برآوردگر بیشینه گر احتمال پسین همانند برآوردگر بیشینه درست نمایی عمل میکند.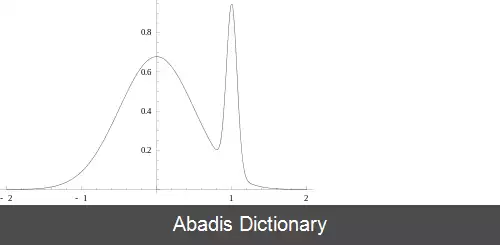
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرآوردگر بیشینه گر احتمال پسین ارتباط نزدیکی با برآورد درستنمایی بیشینه دارد، با این تفاوت که برای پارامتر مورد تخمین احتمال پیشین را هم در نظر می گیرد. در نتیجه، می توان برآوردگر بیشینه گر احتمال پسین را همان برآورد درست نمایی بیشینه دانست به همراه یک تنظیم گر.
فرض کنید میخواهیم پارامتر جمعیت مشاهده نشده ی θ را بر اساس مشاهدات x تخمین بزنیم. فرض کنید f توزیع نمونه گیری x باشد، پس احتمال x وقتی که پارامتر جمعیت θ باشد، f ( x | θ ) است. تابع زیر به تابع درست نمایی معروف است:
θ ↦ f ( x | θ )
و تخمین زیر، برآورد حداکثر درست نمایی است:
θ ^ M L E ( x ) = a r g m a x θ f ( x ∣ θ )
حال فرض کنید توزیع پیشین g روی θ وجود داشته باشد. این کار به ما اجازه می دهد تا با θ به عنوان یک متغیر تصادفی رفتار کنیم. محاسبه ی توزیع پسین θ با استفاده از قانون بیز به صورت زیر است:
θ ↦ f ( θ ∣ x ) = f ( x ∣ θ ) g ( θ ) ∫ Θ f ( x ∣ ϑ ) g ( ϑ ) d ϑ
g تابع چگالی θ و Θ دامنه ی g است.
روش برآوردگر بیشینه گر احتمال پسین به صورت زیر است:
θ ^ M A P ( x ) = a r g m a x θ f ( θ ∣ x ) = a r g m a x θ f ( x ∣ θ ) g ( θ ) ∫ Θ f ( x ∣ ϑ ) g ( ϑ ) d ϑ = a r g m a x θ f ( x ∣ θ ) g ( θ ) .
مخرج کسر بالا همواره مثبت است و نیز وابسته به θ نیست، در نتیجه نقشی در بهینه سازی تابع ندارد. وقتی g تابعی ثابت باشد آن گاه برآوردگر بیشینه گر احتمال پسین همانند برآوردگر بیشینه درست نمایی عمل میکند.

