برآورد درست نمایی بیشینه. در علم آمار برآورد درست نمایی بیشینه که به طور خلاصه به آن MLE ( مخفف عبارت انگلیسی maximum likelihood estimation ) نیز گفته می شود ) روشی برای برآورد فراسنجه های یک مدل آماری است که وقتی بر مجموعه ای از داده ها عملیات انجام می شود به یک مدل آماری منتهی می شود، آنگاه حداکثر درست نمایی می تواند برآوردی از پارامترهای مدل را ارائه دهد. روش درست نمایی بیشینه همانند بسیاری از روش های شناخته شده ی برآورد آماری است.
فرض کنید برای شخصی اطلاعات مربوط به قد زرافه های ماده بالغ موجود در یک جمعیت مهم باشد اما به خاطر محدودیت هزینه یا زمان نتواند قد تک تک این زرافه ها را اندازه بگیرد، وی تنها می داند که این طول قدها به صورت کلی از توزیع نرمال پیروی می کنند ولی سنجه های توزیع را ( میانگین و واریانس ) را نمی داند، در این شرایط وی با استفاده از روش درست نمایی بیشینه و با در دست داشتن اطلاعات مربوط به نمونه ای محدود از جمعیت زرافه ها می تواند تخمینی از میانگین و واریانس قد آن ها را بدست آورد. [ ۱] MLE این کار را به این ترتیب انجام می دهد که واریانس و میانگین را مجهول در نظر می گیرد آنگاه مقادیری را به آن ها نسبت می دهد که با توجه به اطلاعات موجود محتمل ترین حالت باشد. در حالت کلی روش MLE در مورد یک مجموعهٔ مشخص از داده ها عبارتست از نسبت دادن مقادیری به پارامترهای مدل که در نتیجهٔ ان توزیعی تولید شود که بیشترین احتمال را به داده های مشاهده شده نسبت دهد ( یعنی مقادیری از پارامتر که تابع درست نمایی را حداکثر کند ) . MLE یک سازو کار مشخص را برای تخمین ارائه می دهد که در مورد توزیع نرمال و بسیاری توزیع های دیگر به طور خوش تعریف عمل می کند. با این حال در بعضی موارد مشکلاتی پیش می آید از قبیل اینکه برآوردگرهای حداکثر درست نمایی نامناسب اند یا اصلاً وجود ندارند. [ ۲]
فرض کنید n مشاهدهٔ x 1 , x 2 , ⋯ , x n موجود است که به طور مستقل از هم و یکنواخت توزیع شده و از توزیعی با تابع توزیع احتمال نامعلوم ƒ۰ پیروی می کنند. ƒ۰ به طور محتمل متعلق به یک خانواده مشخص از توزیع های نرمال مانند { f ( ⋅ | θ ) , θ ∈ | Θ } می باشد که مدل فراسنجه ای نامیده می شود. بنابراین f 0 = f ( ⋅ ; θ 0 ) و نیز مقدار θ m l e نامعلوم است و به عنوان مقدار درست فراسنجه در نظر گرفته می شود. حال می خواهیم برآورد گری چون θ ^ بیابیم که تا حد امکان به مقدار درست θ 0 نزدیک باشد. هم xi ها و هم فراسنجه θ هر دو می توانند بردار باشند. برای به کارگیری روش درست نمایی بیشینه ابتدا تابع چگالی توام را برای همهٔ مشاهدات تعیین می کنیم. برای حالتی که مشاهدات مستقل و یکنواخت توزیع شده اند، تابع چگالی توام به صورت زیر است: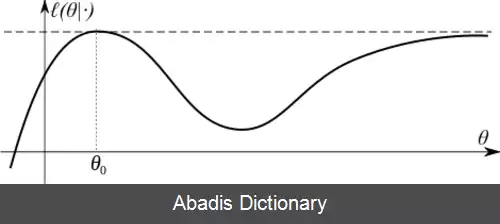
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید برای شخصی اطلاعات مربوط به قد زرافه های ماده بالغ موجود در یک جمعیت مهم باشد اما به خاطر محدودیت هزینه یا زمان نتواند قد تک تک این زرافه ها را اندازه بگیرد، وی تنها می داند که این طول قدها به صورت کلی از توزیع نرمال پیروی می کنند ولی سنجه های توزیع را ( میانگین و واریانس ) را نمی داند، در این شرایط وی با استفاده از روش درست نمایی بیشینه و با در دست داشتن اطلاعات مربوط به نمونه ای محدود از جمعیت زرافه ها می تواند تخمینی از میانگین و واریانس قد آن ها را بدست آورد. [ ۱] MLE این کار را به این ترتیب انجام می دهد که واریانس و میانگین را مجهول در نظر می گیرد آنگاه مقادیری را به آن ها نسبت می دهد که با توجه به اطلاعات موجود محتمل ترین حالت باشد. در حالت کلی روش MLE در مورد یک مجموعهٔ مشخص از داده ها عبارتست از نسبت دادن مقادیری به پارامترهای مدل که در نتیجهٔ ان توزیعی تولید شود که بیشترین احتمال را به داده های مشاهده شده نسبت دهد ( یعنی مقادیری از پارامتر که تابع درست نمایی را حداکثر کند ) . MLE یک سازو کار مشخص را برای تخمین ارائه می دهد که در مورد توزیع نرمال و بسیاری توزیع های دیگر به طور خوش تعریف عمل می کند. با این حال در بعضی موارد مشکلاتی پیش می آید از قبیل اینکه برآوردگرهای حداکثر درست نمایی نامناسب اند یا اصلاً وجود ندارند. [ ۲]
فرض کنید n مشاهدهٔ x 1 , x 2 , ⋯ , x n موجود است که به طور مستقل از هم و یکنواخت توزیع شده و از توزیعی با تابع توزیع احتمال نامعلوم ƒ۰ پیروی می کنند. ƒ۰ به طور محتمل متعلق به یک خانواده مشخص از توزیع های نرمال مانند { f ( ⋅ | θ ) , θ ∈ | Θ } می باشد که مدل فراسنجه ای نامیده می شود. بنابراین f 0 = f ( ⋅ ; θ 0 ) و نیز مقدار θ m l e نامعلوم است و به عنوان مقدار درست فراسنجه در نظر گرفته می شود. حال می خواهیم برآورد گری چون θ ^ بیابیم که تا حد امکان به مقدار درست θ 0 نزدیک باشد. هم xi ها و هم فراسنجه θ هر دو می توانند بردار باشند. برای به کارگیری روش درست نمایی بیشینه ابتدا تابع چگالی توام را برای همهٔ مشاهدات تعیین می کنیم. برای حالتی که مشاهدات مستقل و یکنواخت توزیع شده اند، تابع چگالی توام به صورت زیر است:


wiki: برآورد درست نمایی بیشینه
