در هندسۀ محاسباتی و نظریۀ گراف هندسی، بتا اسکلت یک گراف بدون جهت است که بر روی مجموعه ای از نقاط هندسۀ اقلیدسی تعریف می شود. دو نقطۀ p و q در صورتی توسط یک یال به یکدیگر متصل می شوند که همۀ زاویه های prq از آستانۀ تعیین شده توسط پارامتر عددی β کمتر باشد.
اگر β یک عدد حقیقی مثبت باشد، زاویۀ θ با استفاده از فرمول زیر بدست می آید:
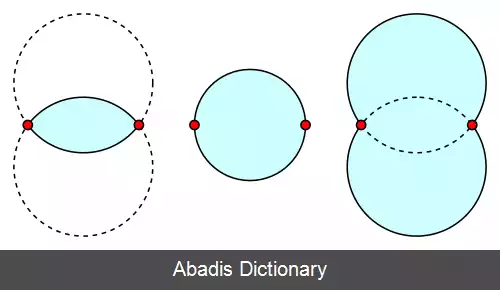
برای هر دو نقطۀ p و q در صفحه، Rpq را مجموعه ای از نقاط در نظر بگیرید به طوری که زاویۀ prq از θ بزرگتر باشد. در این صورت به ازای β ≥ 1 و θ ≤ π/2 مجموعۀ Rpq به صورت اجتماع دو دایره با اندازۀ قطر βd ( p, q ) در خواهد آمد و به ازای β ≤ 1 و θ ≥ π/2 مجموعۀ Rpq به صورت اشتراک دو دایره به قطر d ( p, q ) /β خواهد شد. در صورتی که β = 1 باشد هر دو فرمول بالا جواب θ = π/2 را خواهند داد و مجموعۀ Rpq به صورت یک دایره به قطر pq خواهد شد.
اگر S یک مجموعۀ مجزا از نقاط در صفحۀ هندسۀ اقلیدسی باشد، بتا اسکلت آن یک گراف بدون جهت است که در آن دو نقطۀ p و q در صورتی با یال pq به یکدیگر متصل می شوند که Rpq حاوی هیچ یک از نقاط مجموعۀ S نباشد. در حقیقت بتا اسکلت یک گراف ناحیه خالی می باشد که با ناحیه های Rpq تعریف شده اند. [ ۱] هنگامی که مجموعۀ S شامل نقطۀ r باشد به طوری که زاویۀ prq بزرگتر از θ باشد، pq یال بتا اسکلت نخواهد بود؛ بتا اسکلت شامل آن جفت pq هایی می باشد که همچین نقطۀ r ای برای آن ها وجود نداشته باشد.
بعضی از نویسنده ها تعریف دیگری را بیان می کنند که در آن ناحیه های خالی Rpq به ازای β > 1 اجتماع دو دایره نیستند بلکه عدسی می باشند ( در این متن به آن ها هلال می گوییم ) ، یعنی اشتراک دو دایرۀ متناجس به قطر βd ( p, q ) هستند به طوری که پاره خط pq بر روی شعاع هر دو دایره قرار می گیرد و همچنین دو نقطۀ p و q روی مرز تقاطع دایره ها قرار خواهند گرفت. همانند تعریف مبتنی بر دایره، بتا اسکلت مبتنی بر هلال نیز، در صورتی دارای یال pq می باشد که ناحیۀ Rpq از نقاط دیگر خالی باشد. با توجه به این تعریف، گراف همسایۀ مرتبط یک حالت خاص از بتا اسکلت با β = 2 می باشد. هر دو تعریف مبتنی بر دایره و مبتنی بر هلال به ازای β ≤ 1 یکسانند اما برای مقادیر بزرگ تر β، تعریف بتا اسکلت مبتنی بر دایره زیر گرافی از بتا اسکلت مبتنی بر هلال می باشد.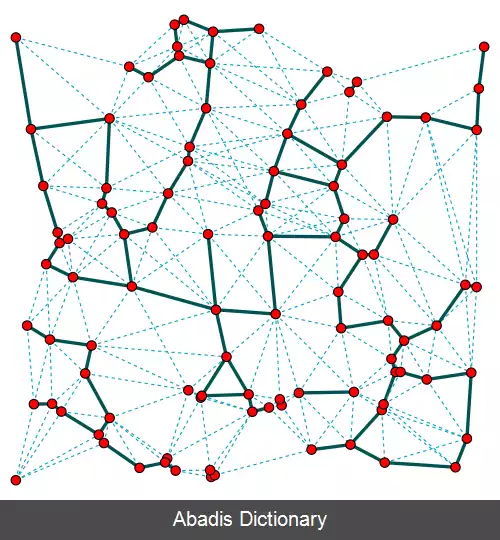
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر β یک عدد حقیقی مثبت باشد، زاویۀ θ با استفاده از فرمول زیر بدست می آید:
برای هر دو نقطۀ p و q در صفحه، Rpq را مجموعه ای از نقاط در نظر بگیرید به طوری که زاویۀ prq از θ بزرگتر باشد. در این صورت به ازای β ≥ 1 و θ ≤ π/2 مجموعۀ Rpq به صورت اجتماع دو دایره با اندازۀ قطر βd ( p, q ) در خواهد آمد و به ازای β ≤ 1 و θ ≥ π/2 مجموعۀ Rpq به صورت اشتراک دو دایره به قطر d ( p, q ) /β خواهد شد. در صورتی که β = 1 باشد هر دو فرمول بالا جواب θ = π/2 را خواهند داد و مجموعۀ Rpq به صورت یک دایره به قطر pq خواهد شد.
اگر S یک مجموعۀ مجزا از نقاط در صفحۀ هندسۀ اقلیدسی باشد، بتا اسکلت آن یک گراف بدون جهت است که در آن دو نقطۀ p و q در صورتی با یال pq به یکدیگر متصل می شوند که Rpq حاوی هیچ یک از نقاط مجموعۀ S نباشد. در حقیقت بتا اسکلت یک گراف ناحیه خالی می باشد که با ناحیه های Rpq تعریف شده اند. [ ۱] هنگامی که مجموعۀ S شامل نقطۀ r باشد به طوری که زاویۀ prq بزرگتر از θ باشد، pq یال بتا اسکلت نخواهد بود؛ بتا اسکلت شامل آن جفت pq هایی می باشد که همچین نقطۀ r ای برای آن ها وجود نداشته باشد.
بعضی از نویسنده ها تعریف دیگری را بیان می کنند که در آن ناحیه های خالی Rpq به ازای β > 1 اجتماع دو دایره نیستند بلکه عدسی می باشند ( در این متن به آن ها هلال می گوییم ) ، یعنی اشتراک دو دایرۀ متناجس به قطر βd ( p, q ) هستند به طوری که پاره خط pq بر روی شعاع هر دو دایره قرار می گیرد و همچنین دو نقطۀ p و q روی مرز تقاطع دایره ها قرار خواهند گرفت. همانند تعریف مبتنی بر دایره، بتا اسکلت مبتنی بر هلال نیز، در صورتی دارای یال pq می باشد که ناحیۀ Rpq از نقاط دیگر خالی باشد. با توجه به این تعریف، گراف همسایۀ مرتبط یک حالت خاص از بتا اسکلت با β = 2 می باشد. هر دو تعریف مبتنی بر دایره و مبتنی بر هلال به ازای β ≤ 1 یکسانند اما برای مقادیر بزرگ تر β، تعریف بتا اسکلت مبتنی بر دایره زیر گرافی از بتا اسکلت مبتنی بر هلال می باشد.


wiki: بتا اسکلت
