بازی علامت دهی
فرهنگستان زبان و ادب
دانشنامه عمومی
در نظریه بازی ها، بازی علامت دهی یک نوع ساده از بازی بیزی پویا است. [ ۱]
این بازی با دو بازیکن که به سیگنال دهنده یا فرستنده ( S ) و دریافت کننده سیگنال یا گیرنده ( R ) است:
• سیگنال دهنده می تواند یکی از چندین نوع ( type ) باشد. t {\displaystyle t} نوع سیگنال دهنده است، که مشخص کننده تابع دستاورد ( payoff function ) سیگنال دهنده می باشد. نوع سیگنال دهنده اطلاعات خصوصی فرستنده است و برای دریافت کننده معلوم نیست.
• گیرنده تنها یک نوع دارد، بنابراین دستاورد عملکرد وی برای هر دو بازیکن شناخته شده است.
این بازی دارای دو مرحله است:
• در مرحله اول، فرستنده بازی می کند. او می تواند یکی از چندین عمل را که «پیام» نامیده می شود، بازی کند. M {\displaystyle M} مجموعه پیام های ممکن است. M = { m 1 , m 2 , m 3 , . . . , m j } {\displaystyle M=\{m_{1}, m_{2}, m_{3}, . . . , m_{j}\}} .
• در مرحله دوم گیرنده بعد از مشاهده پیام فرستنده بازی می کند. A {\displaystyle A} مجموعه اقدامات ممکن است. A = { a 1 , a 2 , a 3 , . . . , a k } {\displaystyle A=\{a_{1}, a_{2}, a_{3}, . . . , a_{k}\}} .
این دو بازیکن دستاوردی ( payoff ) وابسته به نوع سیگنال دهنده، پیام سیگنال دهنده، و عملی که گیرنده انتخاب می کند، کسب می کنند. [ ۲] [ ۳]
مفهوم تعادلی بازی علامت دهی با تعادل بیزی کامل بیان می شود که ترکیبی از تعادل نش بیزی و تعادل زیر بازی کامل است.
یک فرستنده از نوع t j یک پیام m ∗ ( t j ) در مجموعه احتمال توزیع بر روی M می فرستد. ( m ( t j ) نشان دهنده احتمال آن است که نوع t j هر کدام از پیام های درون M را ارسال کند ) گیرنده با مشاهده پیام m یک عمل a ∗ ( m ) در فضای توزیع احتمالی بر روی A را انجام می دهد.
یک بازی اگر هر چهار شرط زیر را داشته باشد، در تعادل بیزی کامل است:
•
• گیرنده باید یک باور بر نوع فرستنده ای که پیام m {\displaystyle m} را فرستاده است داشته باشد. این باورها را می توان به صورت یک توزیع احتمالی μ ( t i | m ) {\displaystyle \mu ( t_{i}|m ) } توصیف کرد، که بیان کننده احتمال آن است که گیرنده نوع t i {\displaystyle t_{i}} پیام m {\displaystyle m} را انتخاب کند. جمع این احتمال بر همه نوع های t i {\displaystyle t_{i}} به شرط هر پیام m {\displaystyle m} باید ۱ باشد.
• عملی که گیرنده انتخاب می کند، با توجه به انتظارات وی نسبت به اینکه چه نوعی از فرستنده پیام m {\displaystyle m} را فرستاده است μ ( t | m ) {\displaystyle \mu ( t|m ) } ، باید بیشینه کننده مطلوبیت انتظاری گیرنده باشد. این یعنی جمع ∑ t i μ ( t i | m ) U R ( t i , m , a ) {\displaystyle \sum _{t_{i}}\mu ( t_{i}|m ) U_{R} ( t_{i}, m, a ) } بیشینه باشد. عمل a {\displaystyle a} که بیشینه کننده جمع است را a ∗ ( m ) {\displaystyle a^{*} ( m ) } می نامیم.
• برای هر نوع t {\displaystyle t} ، فرستنده پیغام m ∗ {\displaystyle m^{*}} را برای ارسال انتخاب می کند، به صورتی که مطلوبیت وی U S ( t , m , a ∗ ( m ) {\displaystyle U_{S} ( t, m, a^{*} ( m ) } با داده شدن استراتژی انتخاب شده گیرنده ( a ∗ {\displaystyle a^{*}} ) ، بیشینه شود.
• برای هر پیام m {\displaystyle m} که فرستنده می تواند ارسال کند، اگر یک نوع t {\displaystyle t} وجود داشته باشد که m ∗ ( t ) {\displaystyle m^{*} ( t ) } یک احتمال اکیداً مثبت به m {\displaystyle m} اختصاص دهد، ( برای هر پیغامی که با احتمال مثبت ارسال می شود ) ، باوری که گیرنده با مشاهده پیام m {\displaystyle m} بر نوع گیرنده دارد μ ( t | m ) {\displaystyle \mu ( t|m ) } ، باید قاعده بیز را رعایت کند. μ ( t | m ) = p ( t ) / ∑ t i p ( t i ) {\displaystyle \mu ( t|m ) =p ( t ) /\sum _{t_{i}}p ( t_{i} ) }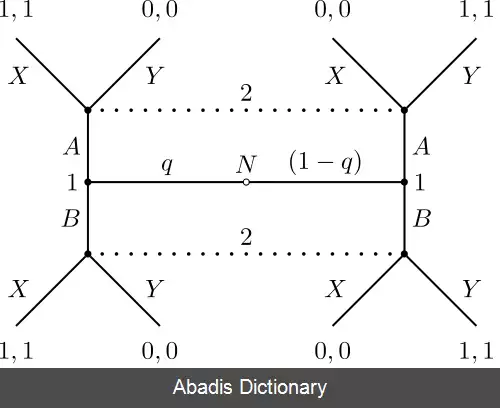
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین بازی با دو بازیکن که به سیگنال دهنده یا فرستنده ( S ) و دریافت کننده سیگنال یا گیرنده ( R ) است:
• سیگنال دهنده می تواند یکی از چندین نوع ( type ) باشد. t {\displaystyle t} نوع سیگنال دهنده است، که مشخص کننده تابع دستاورد ( payoff function ) سیگنال دهنده می باشد. نوع سیگنال دهنده اطلاعات خصوصی فرستنده است و برای دریافت کننده معلوم نیست.
• گیرنده تنها یک نوع دارد، بنابراین دستاورد عملکرد وی برای هر دو بازیکن شناخته شده است.
این بازی دارای دو مرحله است:
• در مرحله اول، فرستنده بازی می کند. او می تواند یکی از چندین عمل را که «پیام» نامیده می شود، بازی کند. M {\displaystyle M} مجموعه پیام های ممکن است. M = { m 1 , m 2 , m 3 , . . . , m j } {\displaystyle M=\{m_{1}, m_{2}, m_{3}, . . . , m_{j}\}} .
• در مرحله دوم گیرنده بعد از مشاهده پیام فرستنده بازی می کند. A {\displaystyle A} مجموعه اقدامات ممکن است. A = { a 1 , a 2 , a 3 , . . . , a k } {\displaystyle A=\{a_{1}, a_{2}, a_{3}, . . . , a_{k}\}} .
این دو بازیکن دستاوردی ( payoff ) وابسته به نوع سیگنال دهنده، پیام سیگنال دهنده، و عملی که گیرنده انتخاب می کند، کسب می کنند. [ ۲] [ ۳]
مفهوم تعادلی بازی علامت دهی با تعادل بیزی کامل بیان می شود که ترکیبی از تعادل نش بیزی و تعادل زیر بازی کامل است.
یک فرستنده از نوع t j یک پیام m ∗ ( t j ) در مجموعه احتمال توزیع بر روی M می فرستد. ( m ( t j ) نشان دهنده احتمال آن است که نوع t j هر کدام از پیام های درون M را ارسال کند ) گیرنده با مشاهده پیام m یک عمل a ∗ ( m ) در فضای توزیع احتمالی بر روی A را انجام می دهد.
یک بازی اگر هر چهار شرط زیر را داشته باشد، در تعادل بیزی کامل است:
•
• گیرنده باید یک باور بر نوع فرستنده ای که پیام m {\displaystyle m} را فرستاده است داشته باشد. این باورها را می توان به صورت یک توزیع احتمالی μ ( t i | m ) {\displaystyle \mu ( t_{i}|m ) } توصیف کرد، که بیان کننده احتمال آن است که گیرنده نوع t i {\displaystyle t_{i}} پیام m {\displaystyle m} را انتخاب کند. جمع این احتمال بر همه نوع های t i {\displaystyle t_{i}} به شرط هر پیام m {\displaystyle m} باید ۱ باشد.
• عملی که گیرنده انتخاب می کند، با توجه به انتظارات وی نسبت به اینکه چه نوعی از فرستنده پیام m {\displaystyle m} را فرستاده است μ ( t | m ) {\displaystyle \mu ( t|m ) } ، باید بیشینه کننده مطلوبیت انتظاری گیرنده باشد. این یعنی جمع ∑ t i μ ( t i | m ) U R ( t i , m , a ) {\displaystyle \sum _{t_{i}}\mu ( t_{i}|m ) U_{R} ( t_{i}, m, a ) } بیشینه باشد. عمل a {\displaystyle a} که بیشینه کننده جمع است را a ∗ ( m ) {\displaystyle a^{*} ( m ) } می نامیم.
• برای هر نوع t {\displaystyle t} ، فرستنده پیغام m ∗ {\displaystyle m^{*}} را برای ارسال انتخاب می کند، به صورتی که مطلوبیت وی U S ( t , m , a ∗ ( m ) {\displaystyle U_{S} ( t, m, a^{*} ( m ) } با داده شدن استراتژی انتخاب شده گیرنده ( a ∗ {\displaystyle a^{*}} ) ، بیشینه شود.
• برای هر پیام m {\displaystyle m} که فرستنده می تواند ارسال کند، اگر یک نوع t {\displaystyle t} وجود داشته باشد که m ∗ ( t ) {\displaystyle m^{*} ( t ) } یک احتمال اکیداً مثبت به m {\displaystyle m} اختصاص دهد، ( برای هر پیغامی که با احتمال مثبت ارسال می شود ) ، باوری که گیرنده با مشاهده پیام m {\displaystyle m} بر نوع گیرنده دارد μ ( t | m ) {\displaystyle \mu ( t|m ) } ، باید قاعده بیز را رعایت کند. μ ( t | m ) = p ( t ) / ∑ t i p ( t i ) {\displaystyle \mu ( t|m ) =p ( t ) /\sum _{t_{i}}p ( t_{i} ) }

wiki: بازی علامت دهی
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
