بازی های ازدحامی دسته ای در نظریهٔ بازی ها هستند که در سال ۱۹۷۳ توسط رزنتال مطرح شدند. در یک بازی ازدحامی بازیکنان و منابع را تعریف می کنیم و سود هر بازیکن به منابعی که انتخاب می کند و تعداد بازیکنانی که همان منابع را انتخاب می کنند بستگی دارد. بازی های ازدحامی حالت خاصی از بازی های پتانسیل می باشند. رزنتال ثابت کرد که هر بازی ازدحامی یک بازی پتانسیل نیز می باشد و بعدها مندرر و شاپلی ( ۱۹۹۶ ) عکس آن را اثبات کردند: به ازای هر بازی پتانسیلی، یک بازی ازدحامی با تابع پتانسیل یکسان موجود است.
یک شبکهٔ ترافیکی را در نظر بگیرید که دو بازیکن از نقطهٔ O حرکت خود را آغاز می کنند و می خواهند به نقطهٔ T برسند. فرض کنید نقطهٔ O با مسیرهای ارتباطی A و B به نقطهٔ T متصل است، به صورتی که مسیر A کمی از مسیر B طول کمتری دارد ( به عبارت دیگر مسیر A با احتمال بیشتری توسط هر بازیکن انتخاب می شود ) . اما هردو راه ارتباطی به سادگی شلوغ می شود؛ به این معنا که هر چه تعداد بازیکن بیشتری از یک مسیر عبور کنند تأخیر هر بازیکن بیشتر می شود. در نتیجه عبور هر دو بازیکن از مسیر یکسان باعث تأخیر اضافی خواهد شد. نتیجهٔ مطلوب در این بازی درصورتی کسب می شود که دو بازیکن همکاری کرده و از مسیرهای متفاوتی عبور کنند. آیا می توان چنین نتیجه ای گرفت؟ و اگر چنین است، هزینهٔ هر بازیکن چه خواهد بود؟
بازی های ازدحامی گسسته دارای اجزای زیرند:
• یک مجموعه از عناصر ازدحام پذیر E {\displaystyle E}
• n {\displaystyle n} بازیکن
• یک مجموعه متناهی از استراتژی های S i {\displaystyle S_{i}} برای هر بازیکن بدین صورت که هر استراتژی P ∈ S i {\displaystyle P\in S_{i}} زیرمجموعه ای از E {\displaystyle E} می باشد.
• به ازای هر عنصر e {\displaystyle e} و یک بردار از استراتژی های ( P 1 , P 2 , … , P n ) {\displaystyle ( P_{1}, P_{2}, \ldots , P_{n} ) } ، باری که این عنصر متحمل می شود به صورت x e = # { i : e ∈ P i } {\displaystyle x_{e}=\#\{i:e\in P_{i}\}} می باشد.
• به ازای هر عنصر e {\displaystyle e} ، یک تابع تأخیر به صورت d e : N ⟶ R {\displaystyle d_{e}:\mathbb {N} \longrightarrow \mathbb {R} }
• به ازای استراتژی P i {\displaystyle P_{i}} داده شده، بازیکن i {\displaystyle i} تأخیری معادل ∑ e ∈ P i d e ( x e ) {\displaystyle \textstyle \sum _{e\in P_{i}}d_{e} ( x_{e} ) } متحمل می شود. فرض کنید که هر d e {\displaystyle d_{e}} مثبت و صعودی به صورت یکنواخت است.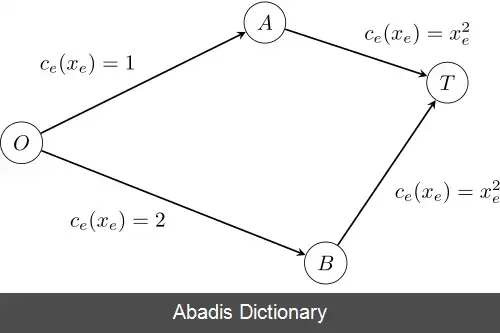
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک شبکهٔ ترافیکی را در نظر بگیرید که دو بازیکن از نقطهٔ O حرکت خود را آغاز می کنند و می خواهند به نقطهٔ T برسند. فرض کنید نقطهٔ O با مسیرهای ارتباطی A و B به نقطهٔ T متصل است، به صورتی که مسیر A کمی از مسیر B طول کمتری دارد ( به عبارت دیگر مسیر A با احتمال بیشتری توسط هر بازیکن انتخاب می شود ) . اما هردو راه ارتباطی به سادگی شلوغ می شود؛ به این معنا که هر چه تعداد بازیکن بیشتری از یک مسیر عبور کنند تأخیر هر بازیکن بیشتر می شود. در نتیجه عبور هر دو بازیکن از مسیر یکسان باعث تأخیر اضافی خواهد شد. نتیجهٔ مطلوب در این بازی درصورتی کسب می شود که دو بازیکن همکاری کرده و از مسیرهای متفاوتی عبور کنند. آیا می توان چنین نتیجه ای گرفت؟ و اگر چنین است، هزینهٔ هر بازیکن چه خواهد بود؟
بازی های ازدحامی گسسته دارای اجزای زیرند:
• یک مجموعه از عناصر ازدحام پذیر E {\displaystyle E}
• n {\displaystyle n} بازیکن
• یک مجموعه متناهی از استراتژی های S i {\displaystyle S_{i}} برای هر بازیکن بدین صورت که هر استراتژی P ∈ S i {\displaystyle P\in S_{i}} زیرمجموعه ای از E {\displaystyle E} می باشد.
• به ازای هر عنصر e {\displaystyle e} و یک بردار از استراتژی های ( P 1 , P 2 , … , P n ) {\displaystyle ( P_{1}, P_{2}, \ldots , P_{n} ) } ، باری که این عنصر متحمل می شود به صورت x e = # { i : e ∈ P i } {\displaystyle x_{e}=\#\{i:e\in P_{i}\}} می باشد.
• به ازای هر عنصر e {\displaystyle e} ، یک تابع تأخیر به صورت d e : N ⟶ R {\displaystyle d_{e}:\mathbb {N} \longrightarrow \mathbb {R} }
• به ازای استراتژی P i {\displaystyle P_{i}} داده شده، بازیکن i {\displaystyle i} تأخیری معادل ∑ e ∈ P i d e ( x e ) {\displaystyle \textstyle \sum _{e\in P_{i}}d_{e} ( x_{e} ) } متحمل می شود. فرض کنید که هر d e {\displaystyle d_{e}} مثبت و صعودی به صورت یکنواخت است.

wiki: بازی ازدحامی
