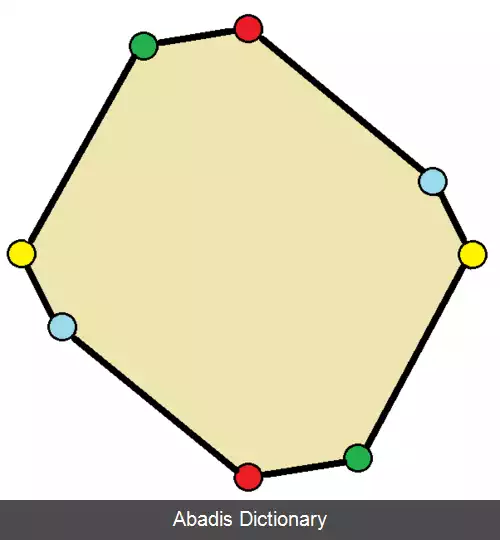
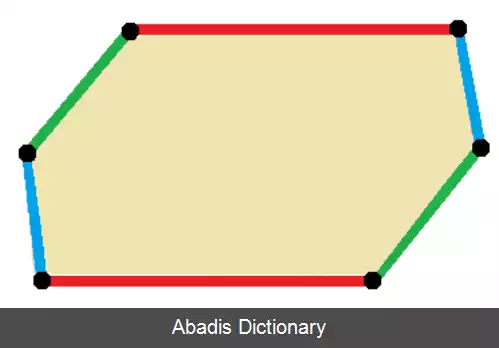
در هندسه، بازتاب نقطه ای ( وارونگی نقطه، وارونگی مرکزی، یا وارونگی از طریق یک نقطه ) نوعی ایزومتریک فضای اقلیدسی است. به جسمی که تحت بازتاب نقطه ای ثابت است، گفته می شود که دارای تقارن نقطه ای است. اگر تحت انعکاس نقطه ای از طریق مرکز خود ثابت باشد، گفته می شود که دارای تقارن مرکزی یا متقارن مرکزی است.
انعکاس نقطه ای را می توان به عنوان یک تبدیل وابسته طبقه بندی کرد. یعنی یک تبدیل آفین ایزومتریک است که دقیقاً یک نقطه ثابت دارد که همان نقطه وارونگی است. معادل یک تبدیل همتتیک با ضریب مقیاس برابر با 1 - است. به نقطه وارونگی مرکز هموتتیک نیز می گویند.
اصطلاح انعکاس سست است و برخی آن را سوء استفاده از زبان می دانند و وارونگی را ترجیح می دهند. با این حال، بازتاب نقطه به طور گسترده ای استفاده می شود. چنین نقشه هایی پیچشی هستند، به این معنی که مرتبه 2 دارند - آنها معکوس خودشان هستند: با اعمال دوبار آنها تابع همانی به دست می آید - که در مورد نقشه های دیگر به نام بازتاب نیز صادق است. به طور دقیق تر، بازتاب به بازتابی در یک ابرصفحه ( 𝑛−1 ) بعدی فضای آفین اشاره دارد - یک نقطه روی خط، یک خط مستقیم در صفحه ( هندسه ) ، یک صفحه در 3 فضا ) ، با ابرصفحه ثابت، اما به طور گسترده تر. بازتاب به هر چرخش فضای اقلیدسی اعمال می شود و مجموعه ثابت ( یک فضای وابسته به بعد k که در آن 1 ≤ k ≤ n − 1 آینه نامیده می شود. در بعد 1 اینها بر هم منطبق هستند، زیرا یک نقطه یک ابر صفحه در خط است.
از نظر جبر خطی، با فرض ثابت بودن مبدأ، چرخش ها دقیقاً نقشه های قطری با همه مقدارویژه و بردارویژه 1 یا - 1 هستند.
انعکاس در یک ابرصفحه دارای یک مقدار ویژه - 1 ( و تعدد n - 1 است. روی 1 مقدار ویژه ) ، در حالی که انعکاس نقطه فقط دارای مقدار ویژه - 1 است ( با تعدد n ) .
اصطلاح وارونگی را نباید با هندسه وارونi اشتباه گرفت، جایی که وارونگی با توجه به یک دایره تعریف می شود.
در دو بعد، بازتاب نقطه ای همان دوران ( هندسه ) 180 درجه است. در سه بعد، یک بازتاب نقطه ای را می توان به عنوان یک چرخش 180 درجه ای توصیف کرد که با انعکاس در سراسر صفحه عمود بر محور چرخش ترکیب تابع شده است. در بعد n، بازتاب های نقطه ای اگر n زوج باشد، جهت گیری را حفظ می کنند و اگر n فرد باشد، جهت گیری را معکوس می کنند.
با توجه به بردار a در فضای اقلیدسی Rn, ، فرمول انعکاس a در سراسر نقطه p است.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفانعکاس نقطه ای را می توان به عنوان یک تبدیل وابسته طبقه بندی کرد. یعنی یک تبدیل آفین ایزومتریک است که دقیقاً یک نقطه ثابت دارد که همان نقطه وارونگی است. معادل یک تبدیل همتتیک با ضریب مقیاس برابر با 1 - است. به نقطه وارونگی مرکز هموتتیک نیز می گویند.
اصطلاح انعکاس سست است و برخی آن را سوء استفاده از زبان می دانند و وارونگی را ترجیح می دهند. با این حال، بازتاب نقطه به طور گسترده ای استفاده می شود. چنین نقشه هایی پیچشی هستند، به این معنی که مرتبه 2 دارند - آنها معکوس خودشان هستند: با اعمال دوبار آنها تابع همانی به دست می آید - که در مورد نقشه های دیگر به نام بازتاب نیز صادق است. به طور دقیق تر، بازتاب به بازتابی در یک ابرصفحه ( 𝑛−1 ) بعدی فضای آفین اشاره دارد - یک نقطه روی خط، یک خط مستقیم در صفحه ( هندسه ) ، یک صفحه در 3 فضا ) ، با ابرصفحه ثابت، اما به طور گسترده تر. بازتاب به هر چرخش فضای اقلیدسی اعمال می شود و مجموعه ثابت ( یک فضای وابسته به بعد k که در آن 1 ≤ k ≤ n − 1 آینه نامیده می شود. در بعد 1 اینها بر هم منطبق هستند، زیرا یک نقطه یک ابر صفحه در خط است.
از نظر جبر خطی، با فرض ثابت بودن مبدأ، چرخش ها دقیقاً نقشه های قطری با همه مقدارویژه و بردارویژه 1 یا - 1 هستند.
انعکاس در یک ابرصفحه دارای یک مقدار ویژه - 1 ( و تعدد n - 1 است. روی 1 مقدار ویژه ) ، در حالی که انعکاس نقطه فقط دارای مقدار ویژه - 1 است ( با تعدد n ) .
اصطلاح وارونگی را نباید با هندسه وارونi اشتباه گرفت، جایی که وارونگی با توجه به یک دایره تعریف می شود.
در دو بعد، بازتاب نقطه ای همان دوران ( هندسه ) 180 درجه است. در سه بعد، یک بازتاب نقطه ای را می توان به عنوان یک چرخش 180 درجه ای توصیف کرد که با انعکاس در سراسر صفحه عمود بر محور چرخش ترکیب تابع شده است. در بعد n، بازتاب های نقطه ای اگر n زوج باشد، جهت گیری را حفظ می کنند و اگر n فرد باشد، جهت گیری را معکوس می کنند.
با توجه به بردار a در فضای اقلیدسی Rn, ، فرمول انعکاس a در سراسر نقطه p است.




wiki: بازتاب نقطه ای
