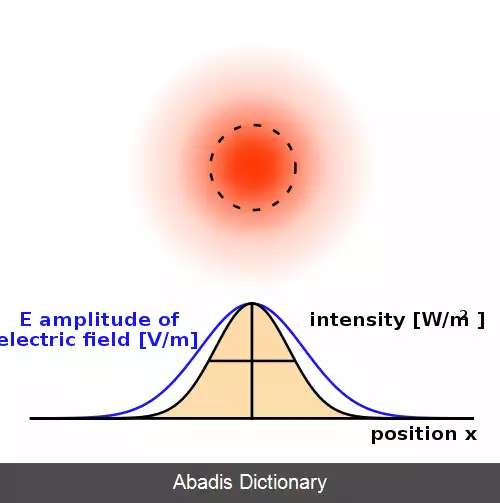
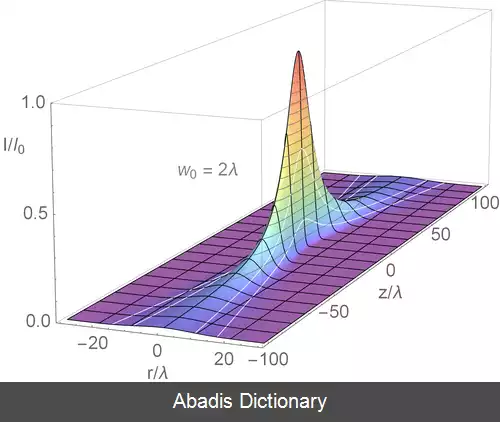
در اپتیک، باریکه گاوسی ( به انگلیسی: Gaussian beam ) باریکه ای از تابش الکترومغناطیسی با تک فامی بالا است که پوش دامنه آن در صفحه عرضی با تابع گاوسی به دست می آید. این همچنین دلالت بر نمایه شدت ( چگالی تابش ) گاوسی دارد. این مُد گاوسی عرضی اصلی ( یا TEM00 ) خروجی مورد نظر اکثر لیزرها ( و نه همه ) را توصیف می کند، زیرا چنین باریکه ای می تواند به متمرکزترین نقطه متمرکز شود. هنگامی که چنین باریکه ای توسط یک عدسی مجدداً فوکوس می شود، وابستگی فاز عرضی تغییر می کند. این منجر به یک باریکه گاوسی متفاوت می شود. نیم نمای دامنه میدان الکتریکی و مغناطیسی در امتداد هر باریکه دایره ای گاوسی ( برای طول موج و قطبش معین ) توسط یک تک پارامتر مشخص می شود: به اصطلاح کمر w0. در هر موقعیت z نسبت به کمر ( تمرکز ) در امتداد باریکه با w0 مشخص شده، دامنه و فازهای میدان بدینوسیله[ ۱] به شرح زیر تعیین می شوند.
راه حل های دلخواه معادله هلمهولتز پیرامحوری را می توان به صورت ترکیبی از مدهای هرمیتی - گاوسی ( که نیم نماهای دامنه با استفاده از مختصات دکارتی در x و y تفکیک پذیر هستند ) ، مدهای لاگر - گاوسی ( که نیم نماهای دامنه در مختصات استوانه ای r و θ تفکیک پذیر هستند ) بیان کرد. یا به طور مشابه به عنوان ترکیبی از مدهای اینس - گاوسی ( که نمایه های دامنه در ξ و η با استفاده از مختصات بیضوی تفکیک پذیر هستند ) . [ ۲] [ ۳] [ ۴]
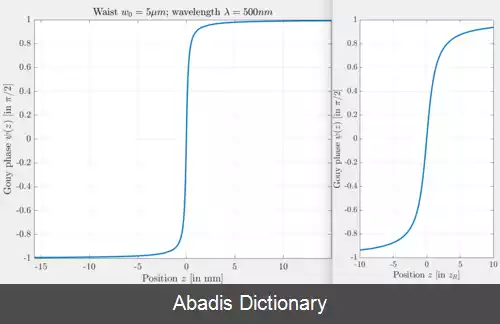
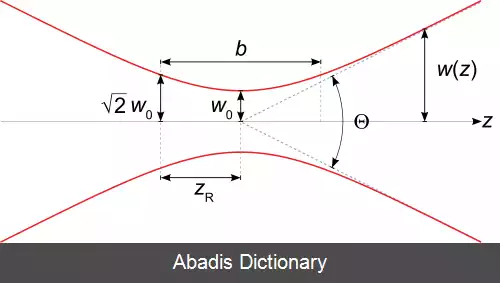
باریکه گاوسی یک مد الکترومغناطیسی عرضی ( TEM ) است. [ ۵] عبارت ریاضی دامنه میدان الکتریکی جوابی برای معادله هلمهولتز پیرامحوری است. [ ۱] با فرض قطبش در جهت x و انتشار در جهت +z، میدان الکتریکی در نماد فازور ( مختلط ) به صورت زیر به دست می آید: E ( r , z ) = E 0 x ^ w 0 w ( z ) exp ( − r 2 w ( z ) 2 ) exp ( − i ( k z + k r 2 2 R ( z ) − ψ ( z ) ) ) که[ ۱] r فاصله شعاعی از محور مرکزی باریکه است، z فاصله محوری از کانون باریکه ( یا "کمر" ) است. i یکه موهومی است، k = ۲πn/λ عدد موج ( برحسب رادیان بر متر ) برای طول موج فضای آزاد λ است و n ضریب شکست محیطی است که باریکه در آن منتشر می شود، E0 = E ( 0, 0 ) , دامنه میدان الکتریکی ( و فاز ) در مبدأ ( r = ۰، z = ۰ ) ، w ( z ) شعاعی است که در آن دامنه میدان به 1/e از مقادیر محوری خود می رسد ( یعنی جایی که مقادیر شدت به 1/e2 از مقادیر محوری خود می رسد ) ، در صفحه z در امتداد باریکه، w0 = w ( 0 ) شعاع کمر است، R ( z ) شعاع انحنای جبهه موج باریکه در z است و ψ ( z ) فاز گویی در z است، جمله فاز اضافی فراتر که مربوط به سرعت فاز نور است. همچنین یک وابستگی زمانی قابل درک وجود دارد eiωt کمیت های فازوری را ضرب می کند. میدان واقعی در یک نقطه از زمان و مکان توسط بخش حقیقی آن کمیت مختلط به دست می آید. این عامل زمان شامل یک قرارداد علامت دلخواه است.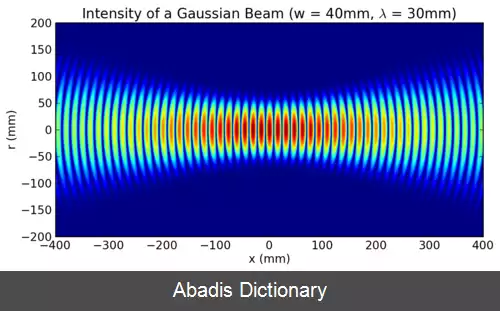

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفراه حل های دلخواه معادله هلمهولتز پیرامحوری را می توان به صورت ترکیبی از مدهای هرمیتی - گاوسی ( که نیم نماهای دامنه با استفاده از مختصات دکارتی در x و y تفکیک پذیر هستند ) ، مدهای لاگر - گاوسی ( که نیم نماهای دامنه در مختصات استوانه ای r و θ تفکیک پذیر هستند ) بیان کرد. یا به طور مشابه به عنوان ترکیبی از مدهای اینس - گاوسی ( که نمایه های دامنه در ξ و η با استفاده از مختصات بیضوی تفکیک پذیر هستند ) . [ ۲] [ ۳] [ ۴]
باریکه گاوسی یک مد الکترومغناطیسی عرضی ( TEM ) است. [ ۵] عبارت ریاضی دامنه میدان الکتریکی جوابی برای معادله هلمهولتز پیرامحوری است. [ ۱] با فرض قطبش در جهت x و انتشار در جهت +z، میدان الکتریکی در نماد فازور ( مختلط ) به صورت زیر به دست می آید: E ( r , z ) = E 0 x ^ w 0 w ( z ) exp ( − r 2 w ( z ) 2 ) exp ( − i ( k z + k r 2 2 R ( z ) − ψ ( z ) ) ) که[ ۱] r فاصله شعاعی از محور مرکزی باریکه است، z فاصله محوری از کانون باریکه ( یا "کمر" ) است. i یکه موهومی است، k = ۲πn/λ عدد موج ( برحسب رادیان بر متر ) برای طول موج فضای آزاد λ است و n ضریب شکست محیطی است که باریکه در آن منتشر می شود، E0 = E ( 0, 0 ) , دامنه میدان الکتریکی ( و فاز ) در مبدأ ( r = ۰، z = ۰ ) ، w ( z ) شعاعی است که در آن دامنه میدان به 1/e از مقادیر محوری خود می رسد ( یعنی جایی که مقادیر شدت به 1/e2 از مقادیر محوری خود می رسد ) ، در صفحه z در امتداد باریکه، w0 = w ( 0 ) شعاع کمر است، R ( z ) شعاع انحنای جبهه موج باریکه در z است و ψ ( z ) فاز گویی در z است، جمله فاز اضافی فراتر که مربوط به سرعت فاز نور است. همچنین یک وابستگی زمانی قابل درک وجود دارد eiωt کمیت های فازوری را ضرب می کند. میدان واقعی در یک نقطه از زمان و مکان توسط بخش حقیقی آن کمیت مختلط به دست می آید. این عامل زمان شامل یک قرارداد علامت دلخواه است.






wiki: باریکه گاوسی
