نیروی بحرانی بیشترین نیرویی است که یک ستون می تواند تحمل کند بدون اینکه خم شود و کمانش کند. این بار بحرانی از این فرمول به دست می آید:
به طوری که
لئونارد اویلر که یک ریاضیدان سوئیسی بود در سال ۱۷۵۷ این فرمول را به دست آورد. اگر بار وارده از بار بحرانی کمتر باشد ستون دچار کمانش نخواهد شد و صاف باقی می ماند. نیروی بحرانی بیشترین نیرویی است که سازه تحمل می کند و در عین حال دچار خیز جانبی ( کمانش ) نمی شود. به ازای نیروهای بیشتر از نیروی بحرانی، ستون به طور جانبی خیز برمی دارد. نیروی بحرانی ستون را در یک حالت تعادل ناپایدار قرار می دهد. نیرویی با مقداری فراتر از نیروی بحرانی باعث می شود تا سازه کمانش کند ( توجه شود که کمانش هم نوعی واماندگی است ) . هر چه مقدار نیرویی که فراتر از نیروی بحرانی است بیشتر شود، خیز جانبی تیر بیشتر می شود تا جایی که از جهات دیگر مثلاً از نظر معیار تسلیم دچار واماندگی شود.
در حدود سال ۱۹۰۰ میلادی، جی. بی. جانسون نشان داد که برای تیرهای با نسبت لاغری پایین باید از فرمول جایگزینی استفاده شود.
اویلر با این فرضیات فرمول خود را به دست آورد:[ ۱]
• جنس ستون همگن و ایزوتروپیک ( همسانگرد ) است. ۲. نیروی فشاری وارد بر ستون فقط محوری است. ۳. ستون از تنش اولیه برخوردار نیست. ۴. از وزن ستون صرف نظر می شود. ۵. ستون در ابتدا مستقیم است. ( بار محوری بدون خروج از مرکز ) ۶. اتصالات پینی بدون هیچ اصطکاکی هستند ( ممانی به ستون وارد نمی کنند ) و انتهای ستون ثابت است ( نه خیز برمی دارد و نه می پیچد ) ۷. مقطع ستون در طول تیر ثابت است. ۸. تنش مستقیم در مقایسه با تنش خمشی ناچیز است. ( بار فشاری در محدوده الاستیک است ) ۹. طول ستون در مقایسه با ابعاد سطح مقطع بسیار بزرگ است. ۱۰. ستون فقط در قالب کمانش دچار واماندگی می شود. این در صورتی درست است که تنش وارد بر مقطع ستون از تنش تسلیم کمتر باشد. σ = P c r A = π 2 E ( L e / r ) 2 < σ y {\displaystyle \sigma ={\frac {P_{cr}}{A}}={\frac {\pi ^{2}E}{ ( L_{e}/r ) ^{2}}}< \sigma _{y}}
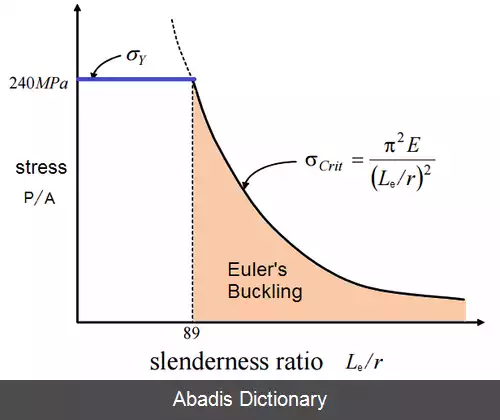
برای تیرهای باریک، تنش ناشی از کمانش معمولاً از تنش تسلیم کمتر است و همچنین در ناحیه الاستیک است. در مقابل، برای یک ستون ضخیم تنش ناشی از کمانش می تواند بیشتر از تنش تسلیم باشد.
داریم:
مدل زیر برای ستونهایی است که در هر انتها پین شده اند ( K = 1 )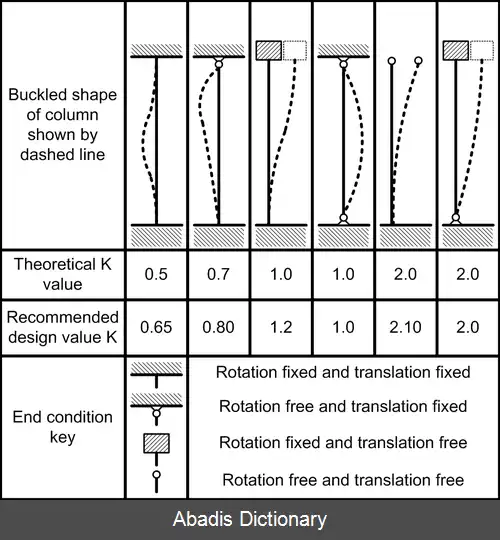

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طوری که
لئونارد اویلر که یک ریاضیدان سوئیسی بود در سال ۱۷۵۷ این فرمول را به دست آورد. اگر بار وارده از بار بحرانی کمتر باشد ستون دچار کمانش نخواهد شد و صاف باقی می ماند. نیروی بحرانی بیشترین نیرویی است که سازه تحمل می کند و در عین حال دچار خیز جانبی ( کمانش ) نمی شود. به ازای نیروهای بیشتر از نیروی بحرانی، ستون به طور جانبی خیز برمی دارد. نیروی بحرانی ستون را در یک حالت تعادل ناپایدار قرار می دهد. نیرویی با مقداری فراتر از نیروی بحرانی باعث می شود تا سازه کمانش کند ( توجه شود که کمانش هم نوعی واماندگی است ) . هر چه مقدار نیرویی که فراتر از نیروی بحرانی است بیشتر شود، خیز جانبی تیر بیشتر می شود تا جایی که از جهات دیگر مثلاً از نظر معیار تسلیم دچار واماندگی شود.
در حدود سال ۱۹۰۰ میلادی، جی. بی. جانسون نشان داد که برای تیرهای با نسبت لاغری پایین باید از فرمول جایگزینی استفاده شود.
اویلر با این فرضیات فرمول خود را به دست آورد:[ ۱]
• جنس ستون همگن و ایزوتروپیک ( همسانگرد ) است. ۲. نیروی فشاری وارد بر ستون فقط محوری است. ۳. ستون از تنش اولیه برخوردار نیست. ۴. از وزن ستون صرف نظر می شود. ۵. ستون در ابتدا مستقیم است. ( بار محوری بدون خروج از مرکز ) ۶. اتصالات پینی بدون هیچ اصطکاکی هستند ( ممانی به ستون وارد نمی کنند ) و انتهای ستون ثابت است ( نه خیز برمی دارد و نه می پیچد ) ۷. مقطع ستون در طول تیر ثابت است. ۸. تنش مستقیم در مقایسه با تنش خمشی ناچیز است. ( بار فشاری در محدوده الاستیک است ) ۹. طول ستون در مقایسه با ابعاد سطح مقطع بسیار بزرگ است. ۱۰. ستون فقط در قالب کمانش دچار واماندگی می شود. این در صورتی درست است که تنش وارد بر مقطع ستون از تنش تسلیم کمتر باشد. σ = P c r A = π 2 E ( L e / r ) 2 < σ y {\displaystyle \sigma ={\frac {P_{cr}}{A}}={\frac {\pi ^{2}E}{ ( L_{e}/r ) ^{2}}}< \sigma _{y}}
برای تیرهای باریک، تنش ناشی از کمانش معمولاً از تنش تسلیم کمتر است و همچنین در ناحیه الاستیک است. در مقابل، برای یک ستون ضخیم تنش ناشی از کمانش می تواند بیشتر از تنش تسلیم باشد.
داریم:
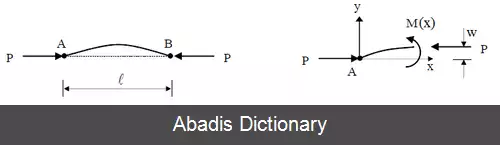
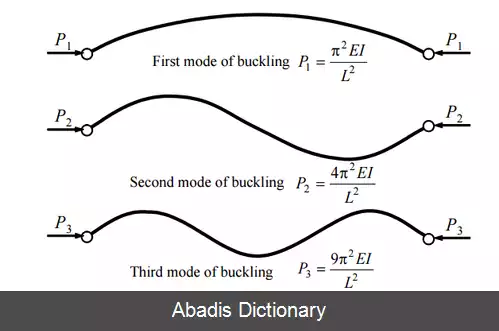
مدل زیر برای ستونهایی است که در هر انتها پین شده اند ( K = 1 )





wiki: بار بحرانی اویلر
