در ریاضیات، اینفیمم یا زیرینه [ ۱] ( مخفّف و نماد آن inf ) یک زیرمجموعه چون از مجموعهٔ با ترتیب جزئی چون ، بزرگترین عنصر درون است که ( در صورت وجود ) کوچکتر یا مساوی با تمام اعضای باشد. [ ۲] لذا عموماً اصطلاح بزرگترین کران پایین ( مخفّف آن GLB ) استفاده می شود. [ ۲]
سوپریمم یا زبرینه [ ۳] ( مخفّف و نماد آن sup ) یک زیرمجموعه چون از یک مجموعهٔ با ترتیب جزئی چون ، کوچکترین عنصری در است که ( در صورت وجود ) بزرگتر یا مساوی با تمام اعضای باشد. [ ۲] لذا، سوپریمم را اغلب کوچکترین کران بالا ( یا LUB ) گویند. [ ۲]
به طور دقیقتر، می توان گفت که اینفیمم دوگان مفهوم سوپریمم است. اینفیمم ها و سوپریمم های اعداد حقیقی حالات خاص رایجی هستند که در آنالیز ریاضی اهمیت دارند، به خصوص در انتگرال گیری لبگ. با این حال، تعاریف عمومی در بستر مباحث مجرّدتر نظریهٔ ترتیب، که در آن مجموعه هایی با ترتیب جزئی دلخواهی در نظر گرفته می شوند همچنان معتبر باقی می مانند.
مفاهیم اینفیمم و سوپریمم به ترتیب مشابه با مفاهیم مینیمم و ماکسیمم هستند، اما در آنالیز اینفیمم و سوپریمم برای مجموعه هایی که مینیمم و ماکسیمم ندارند کاربردی ترند. به عنوان مثال، اعداد حقیقی مثبت R + ( شامل صفر نمی شوند ) مینیمم ندارند، چون هر عنصر از آن را می توان بر دو تقسیم کرد و باز عدد کوچکتری به دست آورد که در آن مجموعه باشد. با این حال، دقیقاً یک اینفیمم از اعداد حقیقی مثبت وجود دارد: 0، که کوچکتر از تمام اعداد حقیقی مثبت بوده و بزرگتر از هر کران پایینی برای این اعداد است.
یک کران پایینِ یک زیرمجموعهٔ S از یک مجموعهٔ جزئی مرتّب P ، یک عنصر a عضو P است به طوری که a ⩽ x ; ∀ x ∈ S .
a ، کران پایین S ، یک زیرینهٔ S نامیده می شود اگر به ازای هر کران پایین y ، y ⩽ a ( a از هر کران پایین دیگری بزرگتر یا مساوی باشد ) .
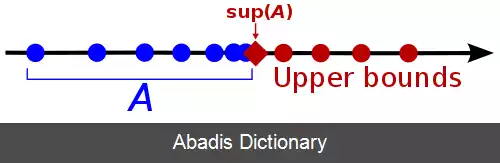
به شکل مشابه، یک کران بالای یک زیرمجموعهٔ S از یک مجموعهٔ جزئی مرتّب P یک عنصر b عضو P است به طوری که b ⩾ x ; ∀ x ∈ S .
b ، کران بالای S ، یک زبرینهٔ S نامیده می شود اگر به ازای هر کران بالای z ، z ⩾ b ( b از هر کران بالای دیگری کوچکتر یا مساوی باشد ) .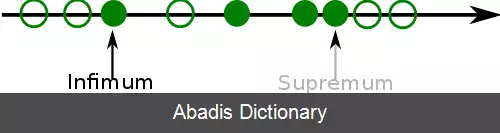
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفسوپریمم یا زبرینه [ ۳] ( مخفّف و نماد آن sup ) یک زیرمجموعه چون از یک مجموعهٔ با ترتیب جزئی چون ، کوچکترین عنصری در است که ( در صورت وجود ) بزرگتر یا مساوی با تمام اعضای باشد. [ ۲] لذا، سوپریمم را اغلب کوچکترین کران بالا ( یا LUB ) گویند. [ ۲]
به طور دقیقتر، می توان گفت که اینفیمم دوگان مفهوم سوپریمم است. اینفیمم ها و سوپریمم های اعداد حقیقی حالات خاص رایجی هستند که در آنالیز ریاضی اهمیت دارند، به خصوص در انتگرال گیری لبگ. با این حال، تعاریف عمومی در بستر مباحث مجرّدتر نظریهٔ ترتیب، که در آن مجموعه هایی با ترتیب جزئی دلخواهی در نظر گرفته می شوند همچنان معتبر باقی می مانند.
مفاهیم اینفیمم و سوپریمم به ترتیب مشابه با مفاهیم مینیمم و ماکسیمم هستند، اما در آنالیز اینفیمم و سوپریمم برای مجموعه هایی که مینیمم و ماکسیمم ندارند کاربردی ترند. به عنوان مثال، اعداد حقیقی مثبت R + ( شامل صفر نمی شوند ) مینیمم ندارند، چون هر عنصر از آن را می توان بر دو تقسیم کرد و باز عدد کوچکتری به دست آورد که در آن مجموعه باشد. با این حال، دقیقاً یک اینفیمم از اعداد حقیقی مثبت وجود دارد: 0، که کوچکتر از تمام اعداد حقیقی مثبت بوده و بزرگتر از هر کران پایینی برای این اعداد است.
یک کران پایینِ یک زیرمجموعهٔ S از یک مجموعهٔ جزئی مرتّب P ، یک عنصر a عضو P است به طوری که a ⩽ x ; ∀ x ∈ S .
a ، کران پایین S ، یک زیرینهٔ S نامیده می شود اگر به ازای هر کران پایین y ، y ⩽ a ( a از هر کران پایین دیگری بزرگتر یا مساوی باشد ) .
به شکل مشابه، یک کران بالای یک زیرمجموعهٔ S از یک مجموعهٔ جزئی مرتّب P یک عنصر b عضو P است به طوری که b ⩾ x ; ∀ x ∈ S .
b ، کران بالای S ، یک زبرینهٔ S نامیده می شود اگر به ازای هر کران بالای z ، z ⩾ b ( b از هر کران بالای دیگری کوچکتر یا مساوی باشد ) .


wiki: اینفیمم و سوپریمم
