در ریاضیات ایزومتری ( انگلیسی: Isometry ) یا طولپا به تبدیلی در فضاهای متری گفته می شود که فاصله نقاط را حفظ می کند. این تبدیل ها معمولاً تناظر دوسویه هستند.
فرض کنیم X و Y فضاهای متری با متریک های dX و dY باشند. یک تابع ƒ : X → Y در صورتی ایزومتری تلقی می شود اگر برای هر a, b ∈ X رابطه زیر برقرار باشد.
• هر بازتاب, انتقال و چرخش در فضای اقلیدسی یک ایزومتری است.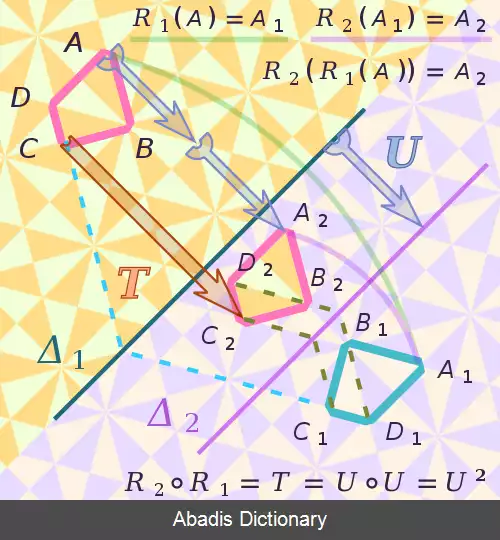
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنیم X و Y فضاهای متری با متریک های dX و dY باشند. یک تابع ƒ : X → Y در صورتی ایزومتری تلقی می شود اگر برای هر a, b ∈ X رابطه زیر برقرار باشد.
• هر بازتاب, انتقال و چرخش در فضای اقلیدسی یک ایزومتری است.

wiki: ایزومتری
