این الگوریتم توسط Hongjun Wu، ارائه شد. رمز دنبالیه ای اچ سی - ۱۲۸ یک نسخهٔ ساده از اچ سی - ۲۵۶ می باشد. الگوریتم HC - ۱۲۸ ساده، امن و در پیاده سازی نرم افزاری کارا است که جزئیات آن به صورت رایگان در دسترس می باشد.
HC - ۱۲۸ حاوی دو جدول مخفی است که هرکدام ۵۱۲ عضو ۳۲ بیتی دارند. در هر مرحله یک عضو از جدول را به وسیلهٔ یک تابع غیر خطی به روزرسانی می کنیم ( پس بعد از ۵۱۲×۲=۱۰۲۴ مرحله تمام اعضای این جداول به روزرسانی می شود ) همچنین در هر مرحله یک خروجی ۳۲ بیتی به وسیلهٔ یک تابع غیر خطی ایجاد می شود. و در نهایت جهت رمز کردن پیام، پیام را با خروجی حاصل از الگوریتم HC - ۱۲۸، جمع ( به پیمانهٔ ۲ ) می کنیم. ( یا به عبارت دیگر پیام را با خروجی این الگوریتم Xor می کنیم. )
در HC - ۱۲۸ وابستگی بین عملیت ها خیلی کم است بنابراین سه مرحلهٔ متوالی در HC - ۱۲۸ را می توان به صورت موازی انجام داد. همچنین در هر مرحله تابع به روز رسانی کننده و تابعی که خروجی را تولید می کند قابلیت این را دارند که به صورت موازی پیاده سازی شوند.
در این قسمت ما به توصیف HC - ۱۲۸ می پردازیم، که با استفاده از یک کلید ۱۲۸ - بیتی ورودی و بردار ۱۲۸ - بیتی اولیه، کلیدی به طول ۲۶۴ تولید می کند.
عملگرهای زیر در HC - ۱۲۸ استفاده شده اند:
دو جدول P و Q در HC - ۱۲۸ استفاده شده است. کلید و بردار اولیه در HC - ۱۲۸ به ترتیب با K و IV نام گذاری شده اند. ما کلیدی که قرار است تولید بشود را با s نمایش می دهیم.
شش تابع در HC - ۱۲۸ استفاده می شود:
f 1 ( x ) = ( x ⋙ 7 ) ⊕ ( x ⋙ 18 ) ⊕ ( x ≫ 3 )
f 2 ( x ) = ( x ⋙ 17 ) ⊕ ( x ⋙ 19 ) ⊕ ( x ≫ 10 )
g 1 ( x , y , z ) = ( ( x ⋙ 10 ) ⊕ ( z ⋙ 23 ) ) + ( y ⋙ 8 )
g 2 ( x , y , z ) = ( ( x ⋘ 10 ) ⊕ ( z ⋘ 23 ) ) + ( y ⋘ 8 )
h 1 ( x ) = Q + Q
h 2 ( x ) = P + P
که x یک کلمهٔ ۳۲ - بیتی به صورت x = x 3 | | x 2 | | x 1 | | x 0 است، 0 ⩽ i < 4 , x i : ( 8 − b i t s ) ، که در آن x 0 کم ارزش ترین بایت و x 3 پر ارزش ترین بایت است.
کلید K و برداراولیه IV را به چهار قسمت مساوی ( هر قسمت ۳۲ - بیت ) به صورت زیر تقسیم می کنیم:
K = K 0 ∥ K 1 ∥ K 2 ∥ K 3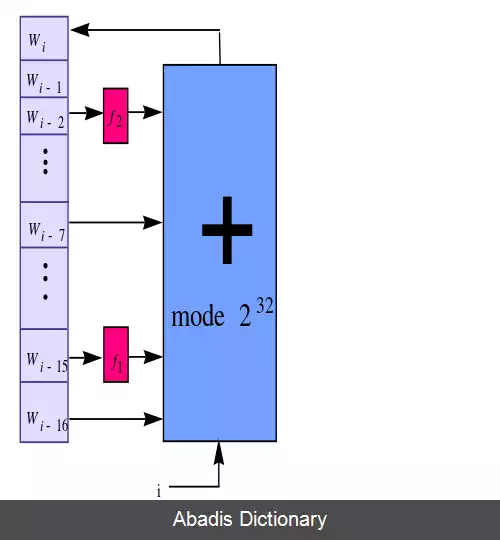
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفHC - ۱۲۸ حاوی دو جدول مخفی است که هرکدام ۵۱۲ عضو ۳۲ بیتی دارند. در هر مرحله یک عضو از جدول را به وسیلهٔ یک تابع غیر خطی به روزرسانی می کنیم ( پس بعد از ۵۱۲×۲=۱۰۲۴ مرحله تمام اعضای این جداول به روزرسانی می شود ) همچنین در هر مرحله یک خروجی ۳۲ بیتی به وسیلهٔ یک تابع غیر خطی ایجاد می شود. و در نهایت جهت رمز کردن پیام، پیام را با خروجی حاصل از الگوریتم HC - ۱۲۸، جمع ( به پیمانهٔ ۲ ) می کنیم. ( یا به عبارت دیگر پیام را با خروجی این الگوریتم Xor می کنیم. )
در HC - ۱۲۸ وابستگی بین عملیت ها خیلی کم است بنابراین سه مرحلهٔ متوالی در HC - ۱۲۸ را می توان به صورت موازی انجام داد. همچنین در هر مرحله تابع به روز رسانی کننده و تابعی که خروجی را تولید می کند قابلیت این را دارند که به صورت موازی پیاده سازی شوند.
در این قسمت ما به توصیف HC - ۱۲۸ می پردازیم، که با استفاده از یک کلید ۱۲۸ - بیتی ورودی و بردار ۱۲۸ - بیتی اولیه، کلیدی به طول ۲۶۴ تولید می کند.
عملگرهای زیر در HC - ۱۲۸ استفاده شده اند:
دو جدول P و Q در HC - ۱۲۸ استفاده شده است. کلید و بردار اولیه در HC - ۱۲۸ به ترتیب با K و IV نام گذاری شده اند. ما کلیدی که قرار است تولید بشود را با s نمایش می دهیم.
شش تابع در HC - ۱۲۸ استفاده می شود:
f 1 ( x ) = ( x ⋙ 7 ) ⊕ ( x ⋙ 18 ) ⊕ ( x ≫ 3 )
f 2 ( x ) = ( x ⋙ 17 ) ⊕ ( x ⋙ 19 ) ⊕ ( x ≫ 10 )
g 1 ( x , y , z ) = ( ( x ⋙ 10 ) ⊕ ( z ⋙ 23 ) ) + ( y ⋙ 8 )
g 2 ( x , y , z ) = ( ( x ⋘ 10 ) ⊕ ( z ⋘ 23 ) ) + ( y ⋘ 8 )
h 1 ( x ) = Q + Q
h 2 ( x ) = P + P
که x یک کلمهٔ ۳۲ - بیتی به صورت x = x 3 | | x 2 | | x 1 | | x 0 است، 0 ⩽ i < 4 , x i : ( 8 − b i t s ) ، که در آن x 0 کم ارزش ترین بایت و x 3 پر ارزش ترین بایت است.
کلید K و برداراولیه IV را به چهار قسمت مساوی ( هر قسمت ۳۲ - بیت ) به صورت زیر تقسیم می کنیم:
K = K 0 ∥ K 1 ∥ K 2 ∥ K 3

wiki: اچ سی ۱۲۸
