آونگ دوتایی. در فیزیک و ریاضیات، در حوزه سامانه های پویا، یک آونگ دوتایی یا آونگ دوگانه ( به انگلیسی: Double pendulum ) آونگی است که آونگ دیگری به انتهای آن متصل است و یک سامانه فیزیکی ساده را تشکیل می دهد که رفتار دینامیکی غنی با حساسیت قوی به شرایط اولیه از خود نشان می دهد. [ ۱] حرکت یک آونگ دوتایی توسط مجموعه ای از معادلات دیفرانسیل معمولی جفت شده کنترل می شود و آشوبناک است.
استفاده از زوایای بین هر بازو و عمود آن به عنوان مختصات تعمیم یافته که پیکربندی دستگاه را تعریف می کند راحت است. این زوایا θ1 و θ2 نشان داده می شوند. موقعیت مرکز جرم هر میله ممکن است برحسب این دو مختصات نوشته شود. اگر مبدأ دستگاه مختصات دکارتی را در نقطه تعلیق اولین آونگ در نظر بگیریم، مرکز جرم این آونگ در زیر است:
x 1 = l 2 sin θ 1 y 1 = − l 2 cos θ 1
و مرکز جرم آونگ دوم است در
x 2 = l ( sin θ 1 + 1 2 sin θ 2 ) y 2 = − l ( cos θ 1 + 1 2 cos θ 2 )
این اطلاعات برای نوشتن لاگرانژی کافی است.
لاگرانژی است L = kinetic energy − potential energy = 1 2 m ( v 1 2 + v 2 2 ) + 1 2 I ( θ ˙ 1 2 + θ ˙ 2 2 ) − m g ( y 1 + y 2 ) = 1 2 m ( x ˙ 1 2 + y ˙ 1 2 + x ˙ 2 2 + y ˙ 2 2 ) + 1 2 I ( θ ˙ 1 2 + θ ˙ 2 2 ) − m g ( y 1 + y 2 ) عبارت اول انرژی جنبشی خطی مرکز جرم جسم ها و جمله دوم انرژی جنبشی دورانی حول مرکز جرم هر میله است. آخرین عبارت انرژی پتانسیل اجسام در یک میدان گرانشی یکنواخت است. علامت نقطه نشان دهنده مشتق زمانی متغیر مورد نظر است.
با جایگزینی مختصات بالا و مرتب کردن مجدد معادله به دست می آید
تنها یک کمیت پایسته ( انرژی ) وجود دارد و هیچ گشتاور پایسته وجود ندارد. دو گشتاور تعمیم یافته ممکن است به صورت نوشته شود
p θ 1 = ∂ L ∂ θ ˙ 1 = 1 6 m l 2 ( 8 θ ˙ 1 + 3 θ ˙ 2 cos ( θ 1 − θ 2 ) ) p θ 2 = ∂ L ∂ θ ˙ 2 = 1 6 m l 2 ( 2 θ ˙ 2 + 3 θ ˙ 1 cos ( θ 1 − θ 2 ) ) .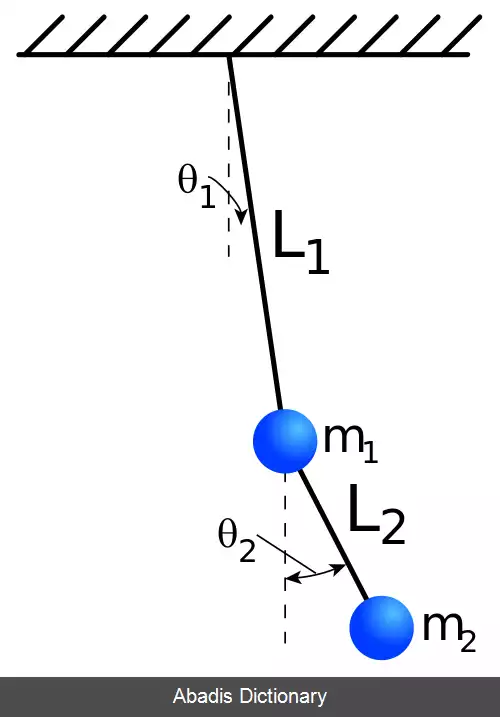
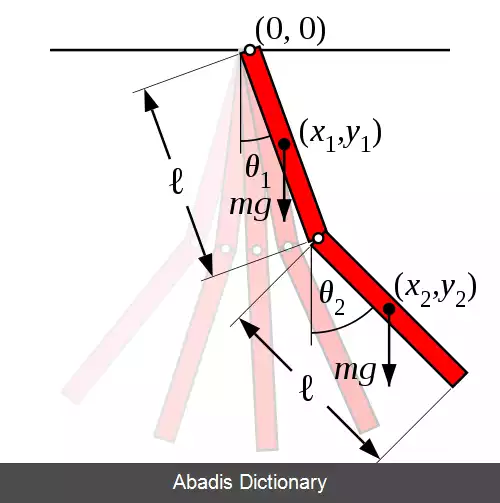

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاستفاده از زوایای بین هر بازو و عمود آن به عنوان مختصات تعمیم یافته که پیکربندی دستگاه را تعریف می کند راحت است. این زوایا θ1 و θ2 نشان داده می شوند. موقعیت مرکز جرم هر میله ممکن است برحسب این دو مختصات نوشته شود. اگر مبدأ دستگاه مختصات دکارتی را در نقطه تعلیق اولین آونگ در نظر بگیریم، مرکز جرم این آونگ در زیر است:
x 1 = l 2 sin θ 1 y 1 = − l 2 cos θ 1
و مرکز جرم آونگ دوم است در
x 2 = l ( sin θ 1 + 1 2 sin θ 2 ) y 2 = − l ( cos θ 1 + 1 2 cos θ 2 )
این اطلاعات برای نوشتن لاگرانژی کافی است.
لاگرانژی است L = kinetic energy − potential energy = 1 2 m ( v 1 2 + v 2 2 ) + 1 2 I ( θ ˙ 1 2 + θ ˙ 2 2 ) − m g ( y 1 + y 2 ) = 1 2 m ( x ˙ 1 2 + y ˙ 1 2 + x ˙ 2 2 + y ˙ 2 2 ) + 1 2 I ( θ ˙ 1 2 + θ ˙ 2 2 ) − m g ( y 1 + y 2 ) عبارت اول انرژی جنبشی خطی مرکز جرم جسم ها و جمله دوم انرژی جنبشی دورانی حول مرکز جرم هر میله است. آخرین عبارت انرژی پتانسیل اجسام در یک میدان گرانشی یکنواخت است. علامت نقطه نشان دهنده مشتق زمانی متغیر مورد نظر است.
با جایگزینی مختصات بالا و مرتب کردن مجدد معادله به دست می آید
تنها یک کمیت پایسته ( انرژی ) وجود دارد و هیچ گشتاور پایسته وجود ندارد. دو گشتاور تعمیم یافته ممکن است به صورت نوشته شود
p θ 1 = ∂ L ∂ θ ˙ 1 = 1 6 m l 2 ( 8 θ ˙ 1 + 3 θ ˙ 2 cos ( θ 1 − θ 2 ) ) p θ 2 = ∂ L ∂ θ ˙ 2 = 1 6 m l 2 ( 2 θ ˙ 2 + 3 θ ˙ 1 cos ( θ 1 − θ 2 ) ) .




wiki: آونگ دوتایی
