آهنگ خرابی. آهنگ شکست یا آهنگ خرابی ( به انگلیسی: Failure rate ) میزانی برای سنجیدن شکست یک سیستم یا مؤلفهٔ مهندسی است، که اغلب بوسیلهٔ حرف یونانی λ ( لاندا ) نشان داده می شود.
آهنگ شکست یک سیستم معمولاً به زمان چرخه حیات آن سیستم بستگی دارد. به عنوان مثال آهنگ شکست یک اتومبیل در پنجمین سال کارکرد آن ممکن است بسیار بیشتر از آهنگ شکست آن در سال اول کارکرد آن باشد.
درعمل میانگین زمان بین شکست اغلب به جای آهنگ شکست به کار می رود. این عمل در صورتی صحیح و قابل استفاده است که آهنگ شکست ثابت باشد.
تعداد کل شکست ها ( خرابی ها ) برای یک جمعیت، تقسیم بر مجموع مدت زمان صرف شده توسط این جمعیت، در طول یک بازه اندازه گیری خاص تحت شرایط معین.
همچنین آهنگ شکست λ ( t ) را می توان احتمال رخ دادن خرابی در یک بازهٔ زمانی مشخص، که قبل از زمان t بدون خرابی بوده است، دانست.
آهنگ شکست در اصل یک احتمال نیست، زیرا مقدار آن می تواند از یک فراتر رود، پس بیان کردن آن به درصد اشتباه خواهد بود، بخصوص اگر آهنگ شکست ما متغیر باشد.
به همین دلیل تابع آهنگ شکست به صورت زیر تعریف می شود
فرض می کنیم متغیر تصادفی X غیر منفی است که طول عمر قطعه ( یا سیستم ) را با تابع چگالی f X ( t ) و تابع توزیع تجمعی F X ( t ) نشان می دهد. آنگاه تابع آهنگ شکست λ X ( t ) ، احتمال پیشامد آن که قطعه یا سیستم تا زمان t خراب نشده باشد و در بازهٔ زمانی ( t , t + d t ) خراب شود را نشان می دهد
λ X ( t ) d t = P { X ∈ ( t , t + d t ) | X > t } = P { X ∈ ( t , t + d t ) ∩ X > t } P { X > t } = P { X ∈ ( t , t + d t ) } P { X > t } = f X ( t ) d t 1 − F X ( t )
در نتیجه تابع آهنگ شکست تعریف می شود
λ X ( t ) ≜ f X ( t ) 1 − F X ( t )
بسیاری از توابع احتمال را می توان برای مدل کردن آهنگ شکست به کار برد. رایج ترین این توابع، تابع توزیع نمایی است :
λ X ( t ) = f X ( t ) 1 − F X ( t ) = λ e − λ t e − λ t = λ
باید توجه داشت که با در اختیار داشتن تابع آهنگ شکست می توان تابع چگالی احتمال و توزیع تجمعی را محاسبه کرد
F X ( x ) = 1 − e − ∫ 0 x λ X ( t ) d t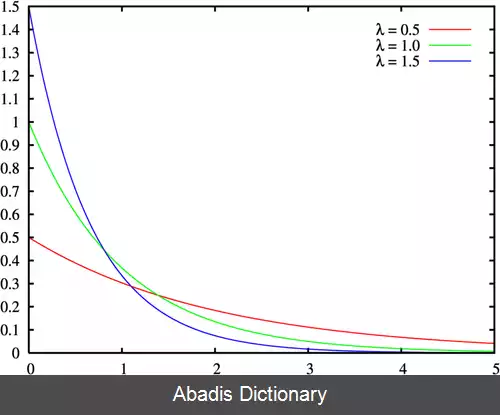
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفآهنگ شکست یک سیستم معمولاً به زمان چرخه حیات آن سیستم بستگی دارد. به عنوان مثال آهنگ شکست یک اتومبیل در پنجمین سال کارکرد آن ممکن است بسیار بیشتر از آهنگ شکست آن در سال اول کارکرد آن باشد.
درعمل میانگین زمان بین شکست اغلب به جای آهنگ شکست به کار می رود. این عمل در صورتی صحیح و قابل استفاده است که آهنگ شکست ثابت باشد.
تعداد کل شکست ها ( خرابی ها ) برای یک جمعیت، تقسیم بر مجموع مدت زمان صرف شده توسط این جمعیت، در طول یک بازه اندازه گیری خاص تحت شرایط معین.
همچنین آهنگ شکست λ ( t ) را می توان احتمال رخ دادن خرابی در یک بازهٔ زمانی مشخص، که قبل از زمان t بدون خرابی بوده است، دانست.
آهنگ شکست در اصل یک احتمال نیست، زیرا مقدار آن می تواند از یک فراتر رود، پس بیان کردن آن به درصد اشتباه خواهد بود، بخصوص اگر آهنگ شکست ما متغیر باشد.
به همین دلیل تابع آهنگ شکست به صورت زیر تعریف می شود
فرض می کنیم متغیر تصادفی X غیر منفی است که طول عمر قطعه ( یا سیستم ) را با تابع چگالی f X ( t ) و تابع توزیع تجمعی F X ( t ) نشان می دهد. آنگاه تابع آهنگ شکست λ X ( t ) ، احتمال پیشامد آن که قطعه یا سیستم تا زمان t خراب نشده باشد و در بازهٔ زمانی ( t , t + d t ) خراب شود را نشان می دهد
λ X ( t ) d t = P { X ∈ ( t , t + d t ) | X > t } = P { X ∈ ( t , t + d t ) ∩ X > t } P { X > t } = P { X ∈ ( t , t + d t ) } P { X > t } = f X ( t ) d t 1 − F X ( t )
در نتیجه تابع آهنگ شکست تعریف می شود
λ X ( t ) ≜ f X ( t ) 1 − F X ( t )
بسیاری از توابع احتمال را می توان برای مدل کردن آهنگ شکست به کار برد. رایج ترین این توابع، تابع توزیع نمایی است :
λ X ( t ) = f X ( t ) 1 − F X ( t ) = λ e − λ t e − λ t = λ
باید توجه داشت که با در اختیار داشتن تابع آهنگ شکست می توان تابع چگالی احتمال و توزیع تجمعی را محاسبه کرد
F X ( x ) = 1 − e − ∫ 0 x λ X ( t ) d t

wiki: آهنگ خرابی
