در ریاضیات، انتگرال یک تابع نامنفی تک متغیره را می توان در ساده ترین حالت، مساحت بین نمودار تابع و محور ایکس ها در نظر گرفت. انتگرال لبگ مفهوم انتگرال گیری را به دسته بزرگتری از توابع گسترش می دهد. همچنین این نوع انتگرال گیری دامنه ای که این توابع بر روی آن ها انتگرال گیری می شوند را نیز گسترش می دهند. در روش انتگرال گیری ریمان، بازه های انتگرال پذیری به تعدادی متناهی زیربازه تقسیم می شد در روش لبگ به مجموعه های کلی تری به نام مجموعه های اندازه پذیر تقسیم می شوند.
خیلی قبل تر از قرن بیستم، ریاضیدانان می دانستند که برای توابع نامنفی که نمودار آن به اندازه کافی هموار باشد، مثل توابع پیوسته بر روی بازه های کراندار بسته، مساحت زیر نمودار را می توان با کمک روش های تقریب زدن با چند ضلعی ها حساب کرد. با این حال همچنان که توجهات بیشتری به سمت توابع نامنظم تر جلب شد ( به عنوان مثال توابعی که از فرایند حد گیری در نظریه احتمال آنالیز ریاضی به وجود می آیند ) ، بیش از پیش مشخص شد که برای تعریف انتگرال گیری از چنین توابعی، نیاز به تکنیک های تقریب محتاطانه تری وجود دارد. همچنین ممکن است بخواهیم بر روی فضاهایی کلی تر از خط حقیقی انتگرال گیری کنیم. انتگرال لبگ تجریدهای لازم برای این کار مهم را فراهم می آورد.
انتگرال لبگ نقش مهمی را در نظریه احتمالات، آنالیز حقیقی، و بسیاری دیگر از زمینه های علوم ریاضی بازی می کند. این انتگرال به افتخار هنری لبگ ( ۱۸۷۵–۱۹۴۱ ) نامگذاری شده که آن را در ۱۹۰۴ معرفی کرد. ( Lebesgue 1904 )
اصطلاح انتگرال گیری لبگ می تواند هم به معنی نظریه کلی انتگرال گیری توابع با توجه به یک اندازه کلی معرفی شده توسط لبگ باشد، یا در حالت خاص تر همان انتگرال گیری توابع روی بخشی از اعداد حقیقی با توجه به اندازه لبگ.
انتگرال یک تابع مثبت مانند f بین کران های a و b را می توان به عنوان مساحت زیر نمودار f تفسیر کرد. فهم این مطلب برای توابع ساده ای چون چند جمله ای ها راحت است، اما در مورد توابع نامتعارف تر چطور؟ در کل، برای چه دسته از توابعی «مساحت زیر نمودار» معنا دارد؟ جواب این سؤال اهمیت نظری و عملی بالایی دارد.
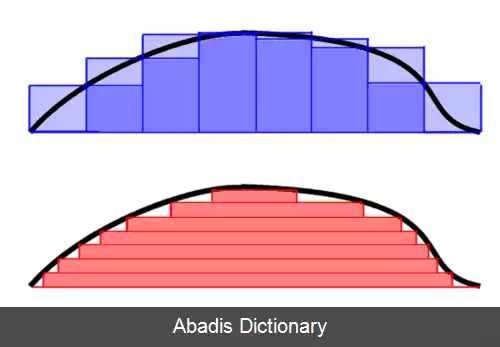
ریاضیدانان در قرن نوزدهم میلادی تلاش کردند تا حساب انتگرالی را به عنوان بخشی از حرکت عمومی به سمت دقت و استحکام ریاضیاتی ( Rigor ) بر روی بنیان های مستحکمی بنا کنند. انتگرال ریمانی که توسط برنهارد ریمان ( ۱۸۲۶ - ۱۸۶۶ ) پیشنهاد شد، یک تلاش موفقیت آمیز گسترده در جهت ارائه چنین بنیانی بود. تعریف ریمان با ساخت دنباله ای از مساحت ها شروع می کند که به راحتی قابل محاسبه اند و جمعشان به انتگرال تابع داده شده همگرا می باشد. این تعریف ازین لحاظ موفق است که برای بسیاری از مسائل از قبل حل شده جواب مورد انتظار را ایجاد کرده و نتایج مفیدی را برای بسیاری از مسائل دیگر ارائه می کند.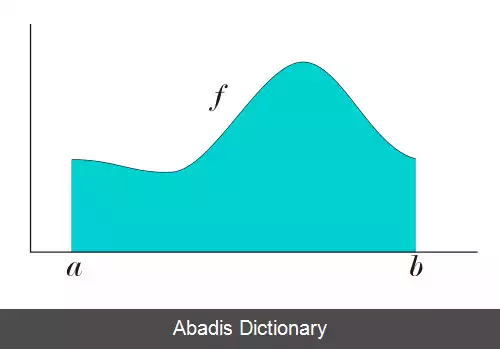
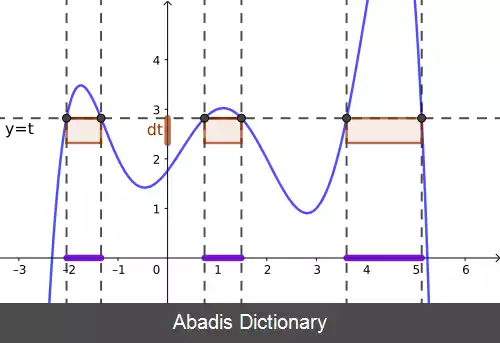
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفخیلی قبل تر از قرن بیستم، ریاضیدانان می دانستند که برای توابع نامنفی که نمودار آن به اندازه کافی هموار باشد، مثل توابع پیوسته بر روی بازه های کراندار بسته، مساحت زیر نمودار را می توان با کمک روش های تقریب زدن با چند ضلعی ها حساب کرد. با این حال همچنان که توجهات بیشتری به سمت توابع نامنظم تر جلب شد ( به عنوان مثال توابعی که از فرایند حد گیری در نظریه احتمال آنالیز ریاضی به وجود می آیند ) ، بیش از پیش مشخص شد که برای تعریف انتگرال گیری از چنین توابعی، نیاز به تکنیک های تقریب محتاطانه تری وجود دارد. همچنین ممکن است بخواهیم بر روی فضاهایی کلی تر از خط حقیقی انتگرال گیری کنیم. انتگرال لبگ تجریدهای لازم برای این کار مهم را فراهم می آورد.
انتگرال لبگ نقش مهمی را در نظریه احتمالات، آنالیز حقیقی، و بسیاری دیگر از زمینه های علوم ریاضی بازی می کند. این انتگرال به افتخار هنری لبگ ( ۱۸۷۵–۱۹۴۱ ) نامگذاری شده که آن را در ۱۹۰۴ معرفی کرد. ( Lebesgue 1904 )
اصطلاح انتگرال گیری لبگ می تواند هم به معنی نظریه کلی انتگرال گیری توابع با توجه به یک اندازه کلی معرفی شده توسط لبگ باشد، یا در حالت خاص تر همان انتگرال گیری توابع روی بخشی از اعداد حقیقی با توجه به اندازه لبگ.
انتگرال یک تابع مثبت مانند f بین کران های a و b را می توان به عنوان مساحت زیر نمودار f تفسیر کرد. فهم این مطلب برای توابع ساده ای چون چند جمله ای ها راحت است، اما در مورد توابع نامتعارف تر چطور؟ در کل، برای چه دسته از توابعی «مساحت زیر نمودار» معنا دارد؟ جواب این سؤال اهمیت نظری و عملی بالایی دارد.
ریاضیدانان در قرن نوزدهم میلادی تلاش کردند تا حساب انتگرالی را به عنوان بخشی از حرکت عمومی به سمت دقت و استحکام ریاضیاتی ( Rigor ) بر روی بنیان های مستحکمی بنا کنند. انتگرال ریمانی که توسط برنهارد ریمان ( ۱۸۲۶ - ۱۸۶۶ ) پیشنهاد شد، یک تلاش موفقیت آمیز گسترده در جهت ارائه چنین بنیانی بود. تعریف ریمان با ساخت دنباله ای از مساحت ها شروع می کند که به راحتی قابل محاسبه اند و جمعشان به انتگرال تابع داده شده همگرا می باشد. این تعریف ازین لحاظ موفق است که برای بسیاری از مسائل از قبل حل شده جواب مورد انتظار را ایجاد کرده و نتایج مفیدی را برای بسیاری از مسائل دیگر ارائه می کند.



wiki: انتگرال لبگ
