انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته می شود. این تعریف را برنهارت ریمان ارائه داد. گرچه انتگرال ریمان دارای محدودیت هایی برای بسیاری از مسائل تئوری است، ولی یکی از ساده ترین روش های تعریف انتگرال بوده و به طور گسترده ای بکار می رود.
تقسیم بازه یک دنباله متناهی به صورت a = x 0 < x 1 < x 2 < ⋯ < x n = b است، که هر یک زیربازه نامیده می شود. اندازه چنین تقسیمی برابر است با طول طولانی ترین زیربازه، یعنی: max ( x i + 1 − x i ) ، 0 ≤ i ≤ n − 1 .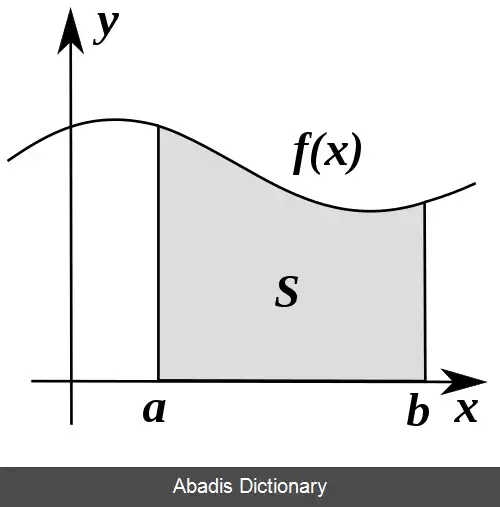

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتقسیم بازه یک دنباله متناهی به صورت a = x 0 < x 1 < x 2 < ⋯ < x n = b است، که هر یک زیربازه نامیده می شود. اندازه چنین تقسیمی برابر است با طول طولانی ترین زیربازه، یعنی: max ( x i + 1 − x i ) ، 0 ≤ i ≤ n − 1 .


wiki: انتگرال ریمان
