انتروپی اطلاعات

آنتروپی اطلاعات. در نظریه اطلاعات، آنتروپی ( به انگلیسی: Entropy ) یا اِنتروپی، معیاری عددی برای اندازه گرفتن اطلاعات، یا تصادفی بودن یک متغیر تصادفی است. به بیان دقیق تر، آنتروپی یک متغیر تصادفی، متوسط اطلاعات آن است. با داشتن یک متغیر تصادفی گسسته X ، که مقادیری از الفبای X می گیرد و از توزیع p : X → پیروی می کند، آنتروپی برای آن به صورت زیر تعریف می شود:
H ( X ) := − ∑ x ∈ X p ( x ) log ⁡ p ( x ) = E
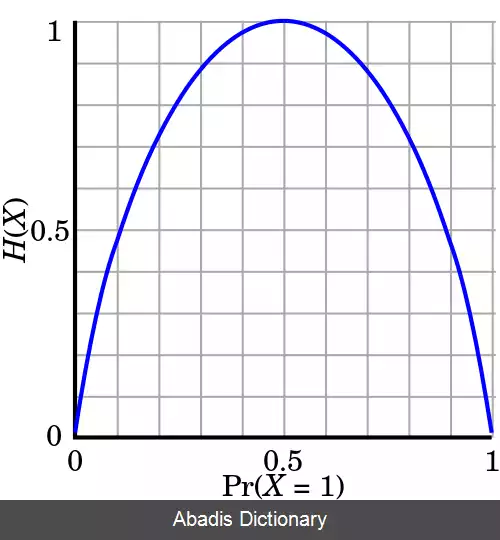
هرچه آنتروپی یک متغیر تصادفی بیشتر باشد، ابهام ما درباره آن بیشتر است؛ به این معنی که پس از مشاهده ی آن، اطلاعات به دست آمده از آن بیشتر خواهد بود.
آنتروپی یک منبع اطلاعات، حد پایین نرخ بهترین فشرده سازی بی اتلاف داده های آن منبع است.
اطلاعات حاصل از مشاهده یک رویداد تصادفی، برابر با منفی لگاریتم احتمال رخ دادن آن تعریف می شود. یک تابع برای اندازه گرفتن اطلاعات یک روی داد تصادفی، ویژگی هایی دارد:
- این که اندازه ی اطلاعات، نامنفی باشد.
- اطلاعات حاصل از مشاهدهٔ یک رویداد قطعی ( یعنی با احتمال برابر با یک ) صفر باشد.
- و مهم تر از همه این که، اطلاعات حاصل از دو مشاهدهٔ مستقل، برابر با جمع اطلاعات حاصل از مشاهدهٔ تک تک آن ها باشد.
می توان نشان داد تنها تابعی که این سه ویژگی را برمی آورد، منفی لگاریتم احتمال است. اندازۀ اطلاعات با تابع لگاریتم در پایه های مختلف، با هم تنها در یک ضریب ثابت اختلاف دارد. متداول ترین پایهٔ لگاریتم در محاسبهٔ اطلاعات، ۲ است که اطلاعات را در واحد بیت محاسبه می کند.
به طور کلی در علوم و مهندسی، آنتروپی معیاری برای ابهام یا بی نظمی است. کلود شانون در مقالهٔ انقلابی خود با نام «A Mathematical Theory of Communication» در ۱۹۴۸، آنتروپی شانون را معرفی کرد و پایه گذار نظریهٔ اطلاعات شد. [ ۱]
آنتروپی در نظریهٔ اطلاعات رابطهٔ تنگاتنگی با مفهوم آنتروپی در ترمودینامیک آماری دارد. این قیاس برخاسته از این است که مقادیر متغیر های تصادفی، انرژی ریزحالت ها را تعیین می کنند و برای همین فرمول گیبز برای آنتروپی به صورت صوری دقیقاً مانند فرمول شانون است. آنتروپی در سایر بخش های ریاضی همچون ترکیبیات و یادگیری ماشین نیز دارای اهمیت است.
ایدهٔ اصلی نظریه اطلاعات این است که «ارزش اطلاعاتی» منتقل شده از طریق یک پیام به میزان غافلگیر کننده بودن این پیام بستگی دارد. اگر یک رویداد بسیار محتمل رخ بدهد، پیام، اطلاعات بسیار کمی را منتقل می کند. در عین حال اگر یک رویداد بسیار غیر محتمل رخ دهد، پیام، اطلاعات آگاه کننده تری را منتقل می کند. برای نمونه، دانش اینکه عددی خاص، عدد برندهٔ یک بخت آزمایی نیست، اطلاع بسیار کمی در اختیار ما قرار می دهد چرا که هر عدد خاص انتخابی به احتمال زیاد برنده نخواهد شد. ولی دانش اینکه عددی خاص برندهٔ بخت آزمایی خواهد بود، ارزش اطلاعاتی زیادی دارد چراکه پیام آن رخداد یک پیامد بسیاد نامحتمل است.