در علوم رایانه، انتخاب سریع یک الگوریتم انتخاب برای پیدا کردن k امین عضو کوچک یک لیست است. همانند مرتب سازی سریع، این الگوریتم نیز توسط تونی هور توسعه داده شده و به همین دلیل به اسم الگوریتم انتخاب تونی هور نیز شناخته می شود. [ ۱] همانند مرتب سازی سریع، این الگوریتم نیز بهینه و دارای عملکرد حالت متوسط خوبی می باشد، اما عملکرد بدترین حالت ممکن این الگوریتم ضعیف است. انتخاب سریع و انواع دیگر آن از جمله الگوریتم های انتخابی هستند که در پیاده سازی های بهینه شده مورد استفاده قرار می گیرند.
انتخاب سریع از رویکرد یکسانی با مرتب سازی سریع بهره می برد، عضوی را به عنوان عنصر محوری انتخاب کرده و داده ها را بر پایهٔ آن به دو قسمت تقسیم می کند ( دو قسمت کمتر و بیشتر از عنصر محوری ) . اگرچه به جای اینکه همانند مرتب سازی سریع بازگشت روی هر دو قسمت داده ها انجام شود، در انتخاب سریع بازگشت تنها روی یکی از این قسمت ها ( قسمتی که دارای عضو k ام است ) انجام می شود. به همین دلیل پیچیدگی این الگوریتم از O ( n l o g n ) به O ( n ) کاهش می یابد.
همانند مرتب سازی سریع، انتخاب سریع نیز معمولاً به صورت الگوریتم درجا پیاده سازی می شود، و علاوه بر پیدا کردن k امین عضو، داده ها را نیز به صورت ناحیه ای مرتب می سازد. برای اطلاعات بیشتر دربارهٔ ارتباط انتخاب سریع با مرتب سازی به الگوریتم انتخاب رجوع کنید.
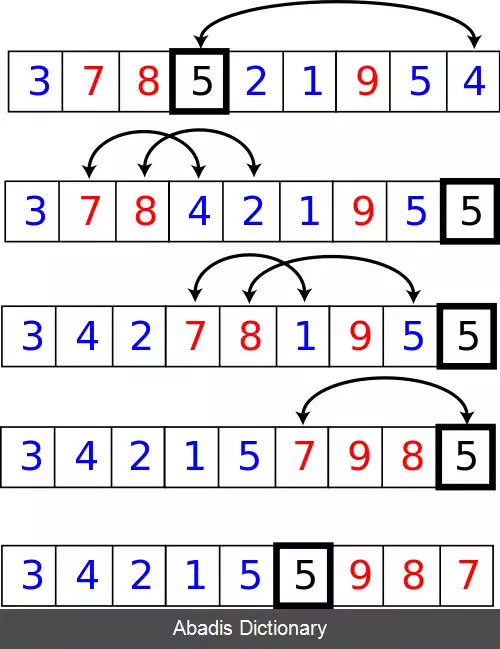
در انتخاب سریع یک زیر رَویه به نام "تقسیم کننده" وجود دارد که می تواند یک لیست را به دو بخش ( اعضای کوچکتر از یک عنصر خاص و اعضای بزرگتر از آن ) تقسیم کند. شبه کد یک تقسیم کننده که یک تقسیم بر پایهٔ [list[pivotIndex انجام می دهد را در زیر می توانید مشاهده کنید:
function partition ( list, left, right, pivotIndex ) pivotValue := list swap list and list // Move pivot to end storeIndex := left for i from left to right - 1 if list < pivotValue swap list and list increment storeIndex swap list and list // Move pivot to its final place return storeIndex در مرتب سازی سریع با مرتب سازی هر قسمت به صورت بازگشتی به عملکردی در بهترین حالت با O ( n l o g n ) دست می یافتیم. در انتخاب سریع از قبل می دانیم که عضو مورد نظر ما در کدام یک از قسمت ها است و به همین دلیل تنها با یک بازگشت در هر مرحله می توانیم به عضو مورد نظر خود برسیم:
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفانتخاب سریع از رویکرد یکسانی با مرتب سازی سریع بهره می برد، عضوی را به عنوان عنصر محوری انتخاب کرده و داده ها را بر پایهٔ آن به دو قسمت تقسیم می کند ( دو قسمت کمتر و بیشتر از عنصر محوری ) . اگرچه به جای اینکه همانند مرتب سازی سریع بازگشت روی هر دو قسمت داده ها انجام شود، در انتخاب سریع بازگشت تنها روی یکی از این قسمت ها ( قسمتی که دارای عضو k ام است ) انجام می شود. به همین دلیل پیچیدگی این الگوریتم از O ( n l o g n ) به O ( n ) کاهش می یابد.
همانند مرتب سازی سریع، انتخاب سریع نیز معمولاً به صورت الگوریتم درجا پیاده سازی می شود، و علاوه بر پیدا کردن k امین عضو، داده ها را نیز به صورت ناحیه ای مرتب می سازد. برای اطلاعات بیشتر دربارهٔ ارتباط انتخاب سریع با مرتب سازی به الگوریتم انتخاب رجوع کنید.
در انتخاب سریع یک زیر رَویه به نام "تقسیم کننده" وجود دارد که می تواند یک لیست را به دو بخش ( اعضای کوچکتر از یک عنصر خاص و اعضای بزرگتر از آن ) تقسیم کند. شبه کد یک تقسیم کننده که یک تقسیم بر پایهٔ [list[pivotIndex انجام می دهد را در زیر می توانید مشاهده کنید:
function partition ( list, left, right, pivotIndex ) pivotValue := list swap list and list // Move pivot to end storeIndex := left for i from left to right - 1 if list < pivotValue swap list and list increment storeIndex swap list and list // Move pivot to its final place return storeIndex در مرتب سازی سریع با مرتب سازی هر قسمت به صورت بازگشتی به عملکردی در بهترین حالت با O ( n l o g n ) دست می یافتیم. در انتخاب سریع از قبل می دانیم که عضو مورد نظر ما در کدام یک از قسمت ها است و به همین دلیل تنها با یک بازگشت در هر مرحله می توانیم به عضو مورد نظر خود برسیم:


wiki: انتخاب سریع
