آمار ناپارامتری. آمار ناپارامتری، در برابر آمار پارامتری، به روش هایی آماری گفته می شود که سعی می کنند کمترین فرض ها را در تحلیل داده انجام دهند. به عبارت دیگر، مدل های آمار ناپارامتری دارای بعد نامتناهی هستند.
آمار ناپارامتری به بررسی مسائل زیر می پردازد:
• تخمین تابع توزیع احتمال: فرض کنید X 1 , … , X n ∼ F {\displaystyle X_{1}, \ldots , X_{n}\sim F} داده شده اند. یک تخمین ناپارامتری برای F {\displaystyle F} توزیع نمونه برداری است:
F ^ n ( X ≤ x ) = 1 n ∑ i = 1 n 1 ( X n ≤ x )
• تخمین تابعکها: یعنی تخمین توابعی که بر حسب تابع توزیع احتمال تعریف شده اند. مانند امید ریاضی و واریانس.
• تخمین تابع چگالی احتمال: یعنی تخمین تابع f = F ′ {\displaystyle f=F'}
• رگرسیون ناپارامتری: نوعی از رگرسیون که هیچ فرضی در مورد توزیع داده نمی کند. مانند رگرسیون بر حسب نزدیکترین همسایه
برای انجام تجزیه و تحلیل های آمار پارامتریک نیاز به یک سری از پیش فرض ها می باشد[ ۱] ؛ که عبارتند از:
• مقیاس داده ها از نوع فاصله ای یا نسبی
• توزیع نرمال داده ها
• همگنی واریانس ها
چنانچه این فرض ها برقرار باشد از آمار پارامتری استفاده می کنیم در غیر اینصورت بایستی از آمار ناپارامتری استفاده نمود. [ ۲]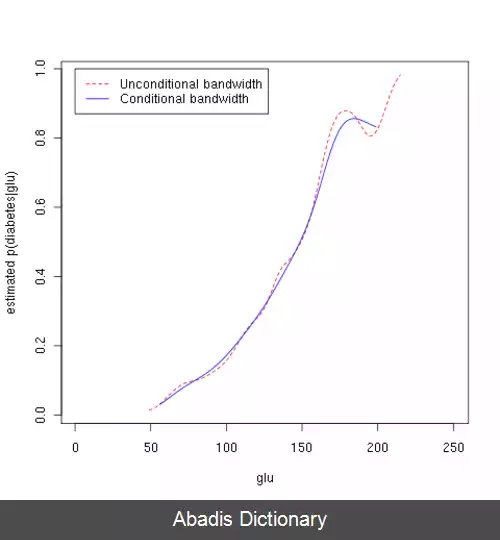
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفآمار ناپارامتری به بررسی مسائل زیر می پردازد:
• تخمین تابع توزیع احتمال: فرض کنید X 1 , … , X n ∼ F {\displaystyle X_{1}, \ldots , X_{n}\sim F} داده شده اند. یک تخمین ناپارامتری برای F {\displaystyle F} توزیع نمونه برداری است:
F ^ n ( X ≤ x ) = 1 n ∑ i = 1 n 1 ( X n ≤ x )
• تخمین تابعکها: یعنی تخمین توابعی که بر حسب تابع توزیع احتمال تعریف شده اند. مانند امید ریاضی و واریانس.
• تخمین تابع چگالی احتمال: یعنی تخمین تابع f = F ′ {\displaystyle f=F'}
• رگرسیون ناپارامتری: نوعی از رگرسیون که هیچ فرضی در مورد توزیع داده نمی کند. مانند رگرسیون بر حسب نزدیکترین همسایه
برای انجام تجزیه و تحلیل های آمار پارامتریک نیاز به یک سری از پیش فرض ها می باشد[ ۱] ؛ که عبارتند از:
• مقیاس داده ها از نوع فاصله ای یا نسبی
• توزیع نرمال داده ها
• همگنی واریانس ها
چنانچه این فرض ها برقرار باشد از آمار پارامتری استفاده می کنیم در غیر اینصورت بایستی از آمار ناپارامتری استفاده نمود. [ ۲]

wiki: آمار ناپارامتری
