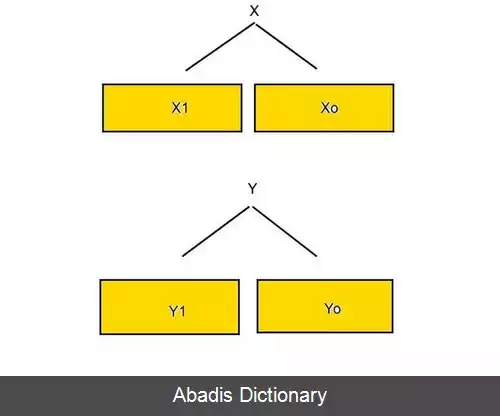
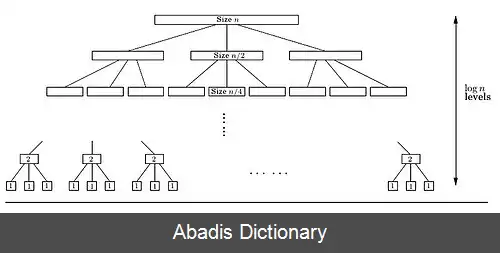
الگوریتم کاراتسوبا یک الگوریتم سریع برای ضرب اعداد است. الگوریتم کاراتسوبا اولین الگوریتمی است که به صورت مجانبی سریع است. این الگوریتم برای اولین بار توسط آناتولی کاراتسوبا در سال ۱۹۶۲ ارائه شد. [ ۱] این الگوریتم با استفاده از روش تقسیم و حل تعداد عملیات ضرب لازم برای ضرب دو عدد n رقمی را کاهش می دهد. در عملیات ضرب معمولی که در دبیرستان آموزش داده می شود، به تعداد n۲ عملیات ضرب لازم است. این الگوریتم تعداد عملیات ضرب را به 3nlog3۲ می رساند. ۳ سال بعد ارائه این الگوریتم توسط کاراتسوبا، الگوریتم Toom - Cook algorithm ارائه شد که حالت کلی تر و سریع تر همین الگوریتم است. علاوه بر این در سال ۱۹۷۱ الگوریتم Schönhage–Strassen algorithm ارائه شد که برای اعداد بزرگ از الگوریتم کاراتسوبا سریع تر است و بهتر عمل می کند.
در سال ۱۹۵۲ آندره کولوموگوروف ادعا کرد که الگوریتم ضرب کلاسیک از نظر پیچیدگی زمانی بهینه است و هر الگوریتم دیگری که برای ضرب دو عدد ارائه شود، حداقل Ω ( n 2 ) عملیات نیاز دارد. سپس در پاییز ۸ سال بعد یعنی سال ۱۹۶۰، در دانشکده مکانیک و ریاضی داشگاه مسکو، سمیناری برگزار و این ادعا را در زمینه پیچیدگی محاسباتی مطرح کرد. [ ۲] در کمتر از یک هفته، کاراتسوبا که در آن زمان ۲۳ ساله بود، الگوریتمی ارائه کرد که به Θ ( n log 2 3 ) عملیات نیاز داشت و به این ترتیب فرضیه کولوموگوروف را رد کرد. او فرضیه خود را بعد از سمینار بعدی با کولوموگوروف در میان گذاشت. کولوموگوروف از این موضوع بسیار آشفته شد، به این خاطر که این الگوریتم به طور کامل نظریهٔ او را رد می کرد. دو سال بعد کولوموگوروف این الگوریتم به صورت مقاله ای کوتاه درآورد و نام کاراتسوبا را در آن قرار داد. نکته جالب توجه آن است که کاراتسوبا پس از انتشار مقاله، از آن باخبر شد. بعد از انتشار این الگوریتم، روشی که کاراتسوبا به کار برد به نام روش تقسیم و حل ( divide and conquer ) نامیده شد. پیدایش روش تقسیم و حل، نقطه شروع نظریه محاسبات سریع بود. پژوهشگرانی مانند توم، کوک و اشتغاسن تلاش های زیادی در این زمینه انجام دادند، که الگوریتم اشتغاسن بهترین الگوریتم از منظر زمان اجرا در این زمینه است. روش تقسیم و حل کاراتسوبا، از پایه ای ترین روش ها در این زمینه است. صدها الگوریتم بر پایهٔ این الگوریتم به وجود آمده اند که مهمترین و مشهورترین آنها، الگوریتم ضرب بر پایه تبدیل سریع فوریه است.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر سال ۱۹۵۲ آندره کولوموگوروف ادعا کرد که الگوریتم ضرب کلاسیک از نظر پیچیدگی زمانی بهینه است و هر الگوریتم دیگری که برای ضرب دو عدد ارائه شود، حداقل Ω ( n 2 ) عملیات نیاز دارد. سپس در پاییز ۸ سال بعد یعنی سال ۱۹۶۰، در دانشکده مکانیک و ریاضی داشگاه مسکو، سمیناری برگزار و این ادعا را در زمینه پیچیدگی محاسباتی مطرح کرد. [ ۲] در کمتر از یک هفته، کاراتسوبا که در آن زمان ۲۳ ساله بود، الگوریتمی ارائه کرد که به Θ ( n log 2 3 ) عملیات نیاز داشت و به این ترتیب فرضیه کولوموگوروف را رد کرد. او فرضیه خود را بعد از سمینار بعدی با کولوموگوروف در میان گذاشت. کولوموگوروف از این موضوع بسیار آشفته شد، به این خاطر که این الگوریتم به طور کامل نظریهٔ او را رد می کرد. دو سال بعد کولوموگوروف این الگوریتم به صورت مقاله ای کوتاه درآورد و نام کاراتسوبا را در آن قرار داد. نکته جالب توجه آن است که کاراتسوبا پس از انتشار مقاله، از آن باخبر شد. بعد از انتشار این الگوریتم، روشی که کاراتسوبا به کار برد به نام روش تقسیم و حل ( divide and conquer ) نامیده شد. پیدایش روش تقسیم و حل، نقطه شروع نظریه محاسبات سریع بود. پژوهشگرانی مانند توم، کوک و اشتغاسن تلاش های زیادی در این زمینه انجام دادند، که الگوریتم اشتغاسن بهترین الگوریتم از منظر زمان اجرا در این زمینه است. روش تقسیم و حل کاراتسوبا، از پایه ای ترین روش ها در این زمینه است. صدها الگوریتم بر پایهٔ این الگوریتم به وجود آمده اند که مهمترین و مشهورترین آنها، الگوریتم ضرب بر پایه تبدیل سریع فوریه است.



wiki: الگوریتم کاراتسوبا
