الگوریتم مرتب سازی

الگوریتم مرتب سازی، در دانش رایانه و ریاضی، الگوریتمی است که فهرستی از داده ها را به ترتیبی مشخص می چیند.
پرکاربردترین ترتیب ها، ترتیب های عددی و واژه نامه ای هستند. مرتب سازی کارا در بهینه سازی الگوریتم هایی که به فهرست های مرتب شده نیاز دارند ( مثل جستجو و ترکیب ) ، اهمیت زیادی دارد.
از آغاز علم رایانه مسائل مرتب سازی بررسی های فراوانی را متوجه خود ساختند؛ شاید به این علت که در عین ساده بودن، حل آن به صورت کارا پیچیده است. برای نمونه مرتب سازی حبابی در سال ۱۹۵۶ به وجود آمد. در حالی که بسیاری این را یک مسئلهٔ حل شده می پندارند، الگوریتم کارآمد جدیدی همچنان ابداع می شوند ( مثلاً مرتب سازی کتابخانه ای در سال ۲۰۰۴ مطرح شد ) .
مبحث مرتب سازی در کلاس های معرفی علم رایانه بسیار پرکاربرد است؛ مبحثی که در آن وجود الگوریتم های فراوان به آشنایی با ایده های کلی و مراحل طراحی الگوریتم های گوناگون کمک می کند؛ مانند تحلیل الگوریتم، داده ساختارها، الگوریتم های تصادفی، تحلیل بدترین و بهترین حالت و حالت میانگین، هزینهٔ زمان و حافظه، و حد پایین.
در این مقاله الگوریتم های مرتب سازی را مقایسه و طبقه بندی می کنیم.
در علم کامپیوتر معمولاً الگوریتم های مرتب سازی بر اساس این معیارها طبقه بندی می شوند:
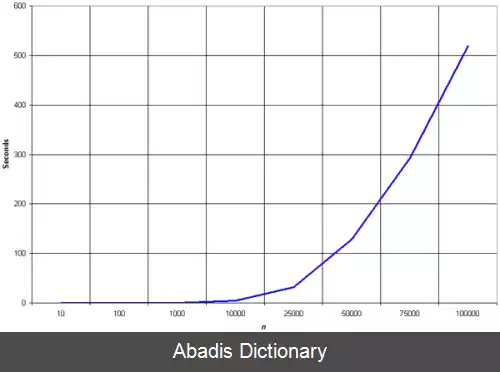
با توجه به اندازهٔ فهرست ( n ) . در مرتب سازی های معمولی عملکرد خوب O ( n log ⁡ n ) و عملکرد بد O ( n 2 ) است. بهترین عملکرد برای مرتب سازی O ( n ) است. الگوریتم هایی که فقط از مقایسهٔ کلیدها استفاده می کنند در حالت میانگین حداقل O ( n log ⁡ n ) مقایسه نیاز دارند.
سرعت الگوریتم مرتب سازی یکی از خصیصه های مهم الگوریتم است که به تعداد مقایسه ها و همچنین تعداد تعویض هایی که باید انجام گیرد، بستگی دارد. سرعت اجرای بعضی از الگوریتم ها با تعداد عناصر لیست نسبت توانی دارد و بعضی دیگر نسبت لگاریتمی. سرعت اجرای الگوریتم در بدترین و بهترین حالت نیز مهم است؛ زیرا ممکن است یکی از این دو حالت برای عمل مرتب سازی انتخاب گردد؛ ممکن است سرعت متوسط اجرای الگوریتم خوب باشد ولی در بدترین حالت سرعت اجرای آن خیلی کم باشد.
بعضی از الگوریتم های مرتب سازی «در جا» هستند. یعنی به جز داده هایی که باید مرتب شوند، حافظهٔ کمی ( O ( 1 ) ) مورد نیاز است؛ در حالی که سایر الگوریتم ها به ایجاد مکان های کمکی در حافظه برای نگه داری اطلاعات موقت نیاز دارند.