الگوریتم فورد - فالکرسون، مسئله بیشینه جریان را در شبکه های جریان حل می کند. این الگوریتم در سال ۱۹۵۶ منتشر شد. نام این الگوریتم به جای الگوریتم ادموندز کارپ هم به کار می رود. ایده اصلی این الگوریتم بسیار ساده است: تا جایی که راهی از منبع ( گره شروع ) به چاهک ( گره پایانی ) ، با یال وزن دار وجود دارد، می توان جریان را از یکی از این مسیرها عبور داد. سپس مسیر دیگری پیدا می شود و همین طور الگوریتم ادامه پیدا می کند.
در گراف داده شده G با ظرفیت c و جریان f ( u، v ) =۰ برای یالی از u به v می خواهیم بیشترین جریان از منبع s به چاهک t را پیدا کنیم. بعد از هر مرحله در الگوریتم موارد زیر پیش می آید:
• f ( u , v ) ≤ c ( u , v ) {\displaystyle f ( u, v ) \leq c ( u, v ) } : جریانی از u {\displaystyle u} به v {\displaystyle v} از ظرفیت بیشتر نمی شود.
• f ( u , v ) = − f ( v , u ) {\displaystyle \ f ( u, v ) = - f ( v, u ) } : شبکه جریان بین u {\displaystyle u} و v {\displaystyle v} را نگهداری می کند.
• ∑ f ( u , v ) = 0 ⟺ f i n ( u ) = f o u t {\displaystyle \sum f ( u, v ) =0\iff f_{in} ( u ) =f_{out}} : به ازای هر گره u {\displaystyle u} به جز چاهک و منبع. مقدار جریان ورودی گره برابر جریان خروجی گره است.
در صورت برقراری این سه شرط، شبکه یک جریان قانونی بعد از هر مرحله خواهد داشت. ما شبکه پسماند را اینگونه تعریف می کنیم، شبکه پسماند G f ( V , E f ) شبکه ایست که ظرفیتش اینگونه بدست می آید: C f ( u , v ) = c ( u , v ) − f ( u , v )
توجه کنید که ممکن است جریانی از v به u وجود داشته باشد، که در شبکه های پسماند قانونی است ولی در شبکه اصلی غیر مجاز است: اگر f ( u، v ) > ۰ و c ( v، u ) =۰ آنگاه cf ( v، u ) > ۰.
• ورودی: گراف G با ظرفیت c، یک منبع s و یک چاه t.
• خروجی: بیشترین جریان f از s به t.
• ۱»برای تمام یال هاf ( u، v ) →۰
• ۲»تا زمانی که مسیر P از s به t در G وجود دارد،
{Cfp=min {cf ( u، v ) | ( u. v ) ϵP را پیدا کن. برای هر یال عضو p داریم f ( u، v ) ⟵ f ( u, v ) + Cfp , f ( v، u ) ⟵ f ( v, u ) - Cfp برای پیدا کردن مسیر در مرحله ۲ می توان از الگوریتم های بی اف اس یا DFS استفاده کرد. وقتی که مسیر دیگری در مرحله ۲ پیدا نشود، s به t در شبکه پشماند نمی رسد. اگر S مجموعه ای از گره های قابل دست رسی برای s در شبکهٔ پشماند باشد، آنگاه مجموع ظرفیت در شبکه اصلی یال ها از S به V در یک طرف برابر است با مجوع جریان هایی از s به t پیدا کرده ایم. این نشان می دهد که بیشترین جریان پیدا شده است.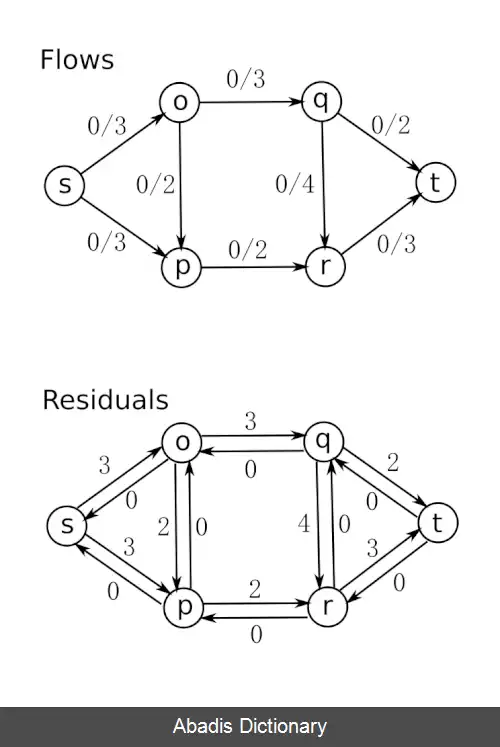

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر گراف داده شده G با ظرفیت c و جریان f ( u، v ) =۰ برای یالی از u به v می خواهیم بیشترین جریان از منبع s به چاهک t را پیدا کنیم. بعد از هر مرحله در الگوریتم موارد زیر پیش می آید:
• f ( u , v ) ≤ c ( u , v ) {\displaystyle f ( u, v ) \leq c ( u, v ) } : جریانی از u {\displaystyle u} به v {\displaystyle v} از ظرفیت بیشتر نمی شود.
• f ( u , v ) = − f ( v , u ) {\displaystyle \ f ( u, v ) = - f ( v, u ) } : شبکه جریان بین u {\displaystyle u} و v {\displaystyle v} را نگهداری می کند.
• ∑ f ( u , v ) = 0 ⟺ f i n ( u ) = f o u t {\displaystyle \sum f ( u, v ) =0\iff f_{in} ( u ) =f_{out}} : به ازای هر گره u {\displaystyle u} به جز چاهک و منبع. مقدار جریان ورودی گره برابر جریان خروجی گره است.
در صورت برقراری این سه شرط، شبکه یک جریان قانونی بعد از هر مرحله خواهد داشت. ما شبکه پسماند را اینگونه تعریف می کنیم، شبکه پسماند G f ( V , E f ) شبکه ایست که ظرفیتش اینگونه بدست می آید: C f ( u , v ) = c ( u , v ) − f ( u , v )
توجه کنید که ممکن است جریانی از v به u وجود داشته باشد، که در شبکه های پسماند قانونی است ولی در شبکه اصلی غیر مجاز است: اگر f ( u، v ) > ۰ و c ( v، u ) =۰ آنگاه cf ( v، u ) > ۰.
• ورودی: گراف G با ظرفیت c، یک منبع s و یک چاه t.
• خروجی: بیشترین جریان f از s به t.
• ۱»برای تمام یال هاf ( u، v ) →۰
• ۲»تا زمانی که مسیر P از s به t در G وجود دارد،
{Cfp=min {cf ( u، v ) | ( u. v ) ϵP را پیدا کن. برای هر یال عضو p داریم f ( u، v ) ⟵ f ( u, v ) + Cfp , f ( v، u ) ⟵ f ( v, u ) - Cfp برای پیدا کردن مسیر در مرحله ۲ می توان از الگوریتم های بی اف اس یا DFS استفاده کرد. وقتی که مسیر دیگری در مرحله ۲ پیدا نشود، s به t در شبکه پشماند نمی رسد. اگر S مجموعه ای از گره های قابل دست رسی برای s در شبکهٔ پشماند باشد، آنگاه مجموع ظرفیت در شبکه اصلی یال ها از S به V در یک طرف برابر است با مجوع جریان هایی از s به t پیدا کرده ایم. این نشان می دهد که بیشترین جریان پیدا شده است.


wiki: الگوریتم فورد–فالکرسون
