در نظریهٔ گراف الگوریتم حذف معکوس ( به انگلیسی: Reverse - delete algorithm ) الگوریتمی است که در یک گراف همبند، با یال وزن دار درخت پوشای کمینه را بدست می آورد. اگر گراف ناهمبند باشد این الگوریتم درخت پوشای کمینه را برای هر مولفهٔ همبندی می یابد که در این صورت مجموعهٔ این درخت های پوشای کمینه را یک جنگل پوشای کمینه گویند.
این الگوریتم الگوریتمی حریصانه است که در هر لحظه بهترین انتخاب را انجام می دهد و برعکس الگوریتم کروسکال که الگوریتم دیگری برای پیدا کردن درخت پوشای کمینه است، عمل می کند. الگوریتم کراسکال با یک گراف خالی شروع می کند و یال ها را به آن اضافه می کند در حالیکه الگوریتم حذف معکوس با گراف اصلی شروع می کند و یال ها را از آن حذف می کند. الگوریتم به صورت زیر عمل می کند:
• با گراف G که لیستی از یال های E دارد شروع کن.
• E را به ترتیب نزولی وزن یال ها مرتب کن.
• برای هر یال چک کن که آیا حذف این یال گراف را ناهمبند می کند یا نه.
• اگر حذف کردن منجر به ناهمبندی گراف نمی شود یال را حذف کن
الگوریتم حذف معکوس این تضمین را می دهد که گراف همبند باقی بماند، چون تنها در صورتی یالی را حذف می کند که باعث ناهمبند شدن گراف نشود. هر یالی که حذف می شود قبل از حذف در دوری شرکت داشته است. از آنجایی که الگوریتم از یال با بیشترین وزن شروع به حذف کردن می کند، آن یال بزرگ ترین یال در دور مربوط به خود است. پس بنابر تعریف درخت پوشای کمینه، یال حذف شده جزء درخت پوشای کمینه نخواهد بود.
1 function ReverseDelete ( edges E ) 2 sort E in decreasing order 3 Define an index i ← 0 4 while i < size ( E ) 5 Define edge temp ← E 6 delete E 7 if temp. v1 is not connected to temp. v2 8 E ← temp 9 i ← i + 1 10 return edges E در بالا گراف، مجوعه یال های وزن دار E است که هر یال آن وزنی دارد و دو راس v1 و v2 را به هم متصل می کند.
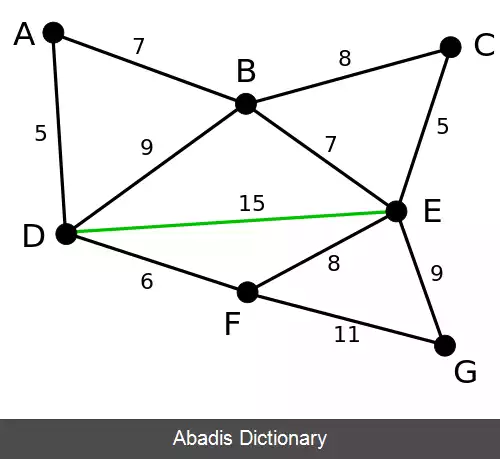
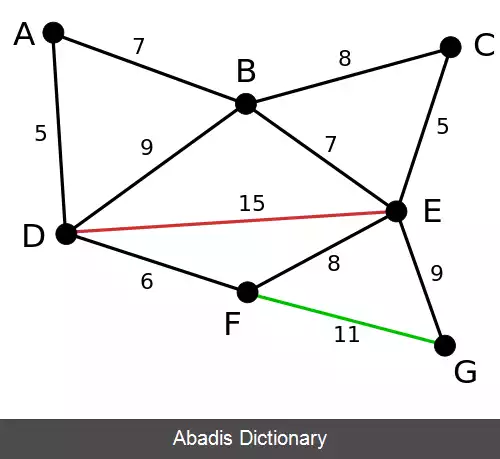
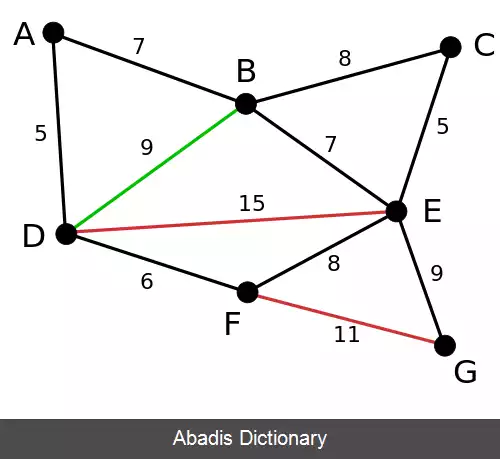
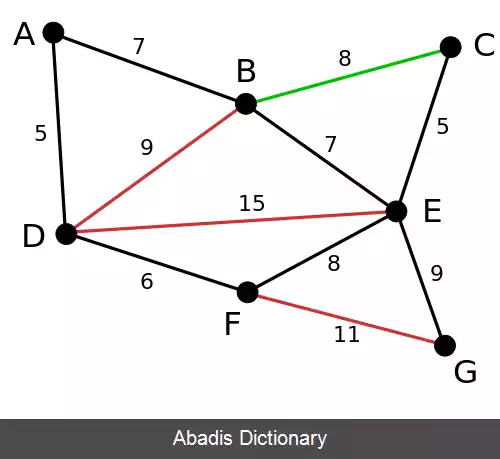
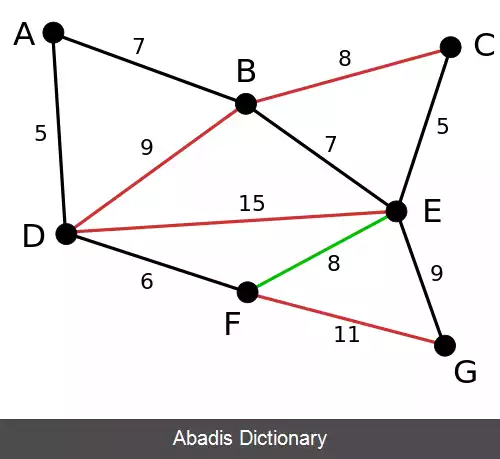
در مثال زیر یال های سبز توسط الگوریتم انتخاب شده اند و یال های قرمز حذف شده اند.
می توان نشان داد که الگوریتم در زمان ( O ( E log E ( log log E ) 3 انجام می شود که E تعداد یال ها و V تعداد گره های گراف است. این حد به صورت زیر محاسبه شده است:
مرتب سازی یال ها با استفاده از الگوریتم مرتب سازی مقایسه ای در زمان ( O ( E log E انجام می گیرد حلقه E بار تکرار می شود.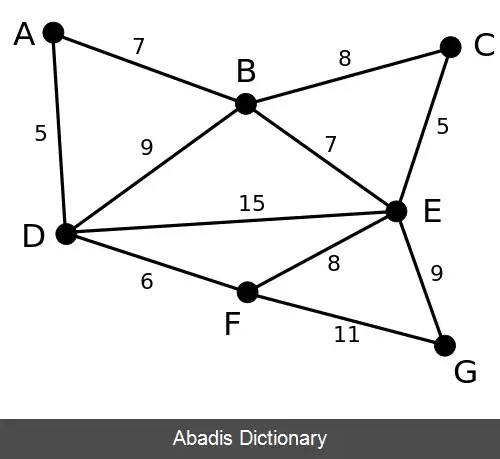
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین الگوریتم الگوریتمی حریصانه است که در هر لحظه بهترین انتخاب را انجام می دهد و برعکس الگوریتم کروسکال که الگوریتم دیگری برای پیدا کردن درخت پوشای کمینه است، عمل می کند. الگوریتم کراسکال با یک گراف خالی شروع می کند و یال ها را به آن اضافه می کند در حالیکه الگوریتم حذف معکوس با گراف اصلی شروع می کند و یال ها را از آن حذف می کند. الگوریتم به صورت زیر عمل می کند:
• با گراف G که لیستی از یال های E دارد شروع کن.
• E را به ترتیب نزولی وزن یال ها مرتب کن.
• برای هر یال چک کن که آیا حذف این یال گراف را ناهمبند می کند یا نه.
• اگر حذف کردن منجر به ناهمبندی گراف نمی شود یال را حذف کن
الگوریتم حذف معکوس این تضمین را می دهد که گراف همبند باقی بماند، چون تنها در صورتی یالی را حذف می کند که باعث ناهمبند شدن گراف نشود. هر یالی که حذف می شود قبل از حذف در دوری شرکت داشته است. از آنجایی که الگوریتم از یال با بیشترین وزن شروع به حذف کردن می کند، آن یال بزرگ ترین یال در دور مربوط به خود است. پس بنابر تعریف درخت پوشای کمینه، یال حذف شده جزء درخت پوشای کمینه نخواهد بود.
1 function ReverseDelete ( edges E ) 2 sort E in decreasing order 3 Define an index i ← 0 4 while i < size ( E ) 5 Define edge temp ← E 6 delete E 7 if temp. v1 is not connected to temp. v2 8 E ← temp 9 i ← i + 1 10 return edges E در بالا گراف، مجوعه یال های وزن دار E است که هر یال آن وزنی دارد و دو راس v1 و v2 را به هم متصل می کند.
در مثال زیر یال های سبز توسط الگوریتم انتخاب شده اند و یال های قرمز حذف شده اند.
می توان نشان داد که الگوریتم در زمان ( O ( E log E ( log log E ) 3 انجام می شود که E تعداد یال ها و V تعداد گره های گراف است. این حد به صورت زیر محاسبه شده است:
مرتب سازی یال ها با استفاده از الگوریتم مرتب سازی مقایسه ای در زمان ( O ( E log E انجام می گیرد حلقه E بار تکرار می شود.






wiki: الگوریتم حذف معکوس
