الگوریتم ادموندز کارپ ( به انگلیسی: Edmonds - Karp algorithm ) : در علوم کامپیوتر و نظریه گراف الگوریتمEdmonds_Karp پیاده سازی ای برای الگوریتم فورد–فالکرسون برای محاسبهٔ مسئله بیشینه جریان در شبکه شاره در زمان O ( | V | | E | 2 ) است. این الگوریتم از الگوریتم ارسال - برچسب که در زمان O ( | V | 3 ) انجام می شود سریع تر است. این الگوریتم اولین بار توسط دانشمند شوروی Yefim ( Chaim ) Dinic در سال ۱۹۷۰[ ۱] منتشر شد؛ و به طور مستقل توسط جک ادموند و ریچارد کارپ در سال ۱۹۷۲[ ۲] با کاهش زمان الگوریتم قبلی به O ( | V | | E | 2 ) انتشار یافته است.
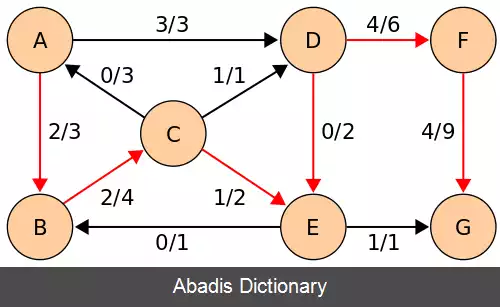
در این اگوریتم می خواهیم بیشینه شاره را از مبدأ s تا مقصد t پیدا کنیم این الگوریتم شبیه به الگوریتم الگوریتم فورد–فالکرسون است و تفاوتش این است که در این الگوریتم محدودیت الگوریتم فورد–فالکرسون بهبود می یابد چرا که که محاسبهٔ مسیر افزایشی را با جستجوی سطح اول پیاده سازی می کنیم. حال آنکه در الگوریتم فورد–فالکرسون جستجوی عمق اول را اجرا می کردیم و به محدودیت زمانی بیشتری نیاز داشت. مسیر پیدا شده باید کوتاه ترین مسیر باشد که ظرفیت آماده ای دارد؛ که توسط جستجوی سطح اول پیدا می شود؛ که ما اجازه می دهیم یال ها اندازهٔ واحدی داشته باشند. بیشترین شاره معادل با برش کمینه است. ویژگی دیگر این الگوریتم این است که طول کوتاه ترین مسیر هر سری افزایش می یابد. اثبات را می توان ار منبع ذکر شده مشاهده کرد[ ۳] کاری که در این الگوریتم می کنیم این است که با جستجوی سطح اول مسیر افزایشی را می یابیم و هر سری اگر که مسیر افزایشی ( مسیری که یال پر ندارداین مسئله هم در کد سطح اولی که در زیر آمده مشخص است ) داشتیم کمترین ظرفیت را پیدا می کند و مینیمم ظرفیت را به جریان همهٔ یال هااضافه می کند و از آن کم می کند. به این صورت بیشینه شار بین مبدأ و مقصد را پیدا می کند که معادل با برش کمینه است. در کد زیر نحوهٔ انجام این الگوریتم نشان داده می شود. ورودی الگوریتم: ورودی این الگوریتم یک گراف است که یک راس مبدأ s دارد و یک راس مقصد t و روی همهٔ یال ها ظرفیت هر یال نوشته شده است. خروجی الگوریتم: بیشترین جریان از s به t تا زمانی که مسیر افزایشی با ویژگی های بالا وجود دارد.
زمان اجرای این الگوریتم O ( | V | | E | 2 ) است. به این علت که هر مسیر در زمان اجرای O ( | E | ) بدست می آید. در هر زمان حداقل یکی از E یال سیر می شوند؛ که فاصله از یال سیر شده تا مبدأ باید طولانی تر از آخرین باری باشد که سیر شده و این طول حداکثر برابر با V تعداد راس ها است.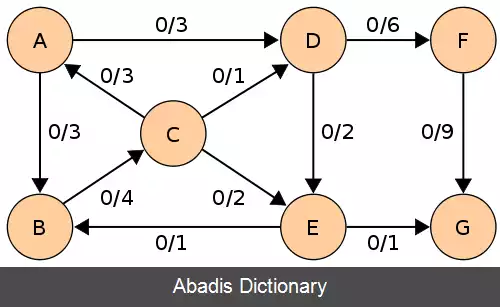
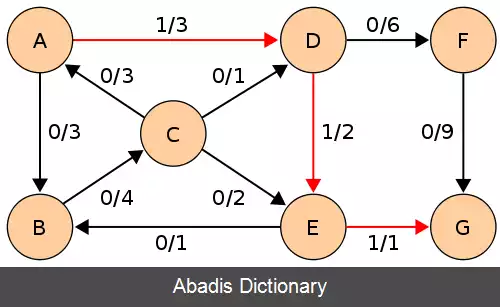
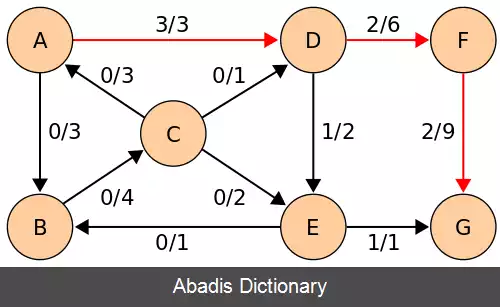
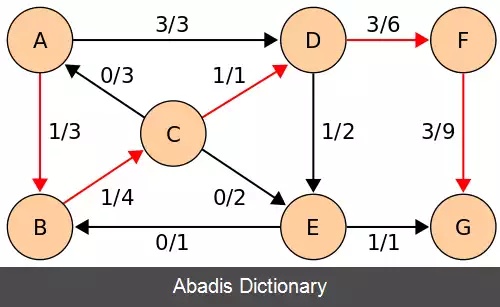

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این اگوریتم می خواهیم بیشینه شاره را از مبدأ s تا مقصد t پیدا کنیم این الگوریتم شبیه به الگوریتم الگوریتم فورد–فالکرسون است و تفاوتش این است که در این الگوریتم محدودیت الگوریتم فورد–فالکرسون بهبود می یابد چرا که که محاسبهٔ مسیر افزایشی را با جستجوی سطح اول پیاده سازی می کنیم. حال آنکه در الگوریتم فورد–فالکرسون جستجوی عمق اول را اجرا می کردیم و به محدودیت زمانی بیشتری نیاز داشت. مسیر پیدا شده باید کوتاه ترین مسیر باشد که ظرفیت آماده ای دارد؛ که توسط جستجوی سطح اول پیدا می شود؛ که ما اجازه می دهیم یال ها اندازهٔ واحدی داشته باشند. بیشترین شاره معادل با برش کمینه است. ویژگی دیگر این الگوریتم این است که طول کوتاه ترین مسیر هر سری افزایش می یابد. اثبات را می توان ار منبع ذکر شده مشاهده کرد[ ۳] کاری که در این الگوریتم می کنیم این است که با جستجوی سطح اول مسیر افزایشی را می یابیم و هر سری اگر که مسیر افزایشی ( مسیری که یال پر ندارداین مسئله هم در کد سطح اولی که در زیر آمده مشخص است ) داشتیم کمترین ظرفیت را پیدا می کند و مینیمم ظرفیت را به جریان همهٔ یال هااضافه می کند و از آن کم می کند. به این صورت بیشینه شار بین مبدأ و مقصد را پیدا می کند که معادل با برش کمینه است. در کد زیر نحوهٔ انجام این الگوریتم نشان داده می شود. ورودی الگوریتم: ورودی این الگوریتم یک گراف است که یک راس مبدأ s دارد و یک راس مقصد t و روی همهٔ یال ها ظرفیت هر یال نوشته شده است. خروجی الگوریتم: بیشترین جریان از s به t تا زمانی که مسیر افزایشی با ویژگی های بالا وجود دارد.
زمان اجرای این الگوریتم O ( | V | | E | 2 ) است. به این علت که هر مسیر در زمان اجرای O ( | E | ) بدست می آید. در هر زمان حداقل یکی از E یال سیر می شوند؛ که فاصله از یال سیر شده تا مبدأ باید طولانی تر از آخرین باری باشد که سیر شده و این طول حداکثر برابر با V تعداد راس ها است.






wiki: الگوریتم ادموندز کارپ
