در ریاضیات، سری فیبوناچی ( به انگلیسی: Fibonacci number ) به دنباله ای از اعداد می گویند که به صورت زیر تعریف می شود:
غیر از دو عدد اول، اعداد بعدی از جمعِ دو عددِ قبلیِ خود به دست می آیند. اولین اعداد این سری عبارت اند از:
این اعداد به نام لئوناردو فیبوناچی، ریاضی دان ایتالیاییِ قرن سیزدهم میلادی، نام گذاری شده است.
در واقع، فیبوناچی در سال ۱۲۰۲ به مسئله عجیبی علاقه مند شد. او می خواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آن ها تعریف کند در نهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود:
• شما یک جفت خرگوش نر و ماده دارید که همین الان به دنیا آمده اند.
• خرگوش ها پس از یک ماه بالغ می شوند.
• دوران بارداری خرگوش ها یک ماه است.
• هنگامی که خرگوش ماده به سن بلوغ می رسد حتماً باردار می شود.
• در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده به دنیا می آورد.
• خرگوش ها هرگز نمی میرند.
حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت؟
فرض کنیم x n تعداد جفت خرگوش پس از n ماه باشد، می دانیم که x 1 = 1 , x 2 = 1 ، تعداد جفت خرگوشها در ماه n + 1 - اُم برابر خواهد بود با حاصل جمع تعداد جفت خرگوش هایی که در این ماه متولد می شوند با تعداد جفت خرگوشهای موجود ( x n ) . اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هم اکنون حداقل دو ماه سن خواهند داشت و به سن زادوولد رسیده اند. تعداد جفت خرگوش های متولد شده برابر خواهد بود با x n − 1 ، پس خواهیم داشت:
x۱ = ۱ , x۲ = ۱ , xn + ۱ = xn + xn - ۱
که اگر از قواعد مذکور پیروی کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است.
۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴, …
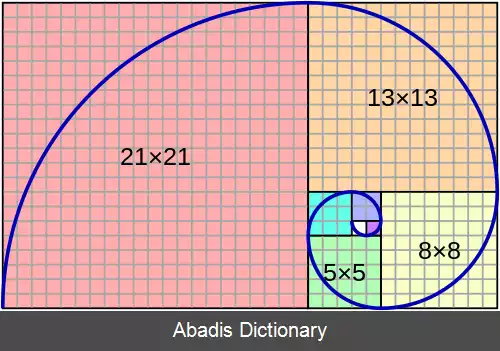
فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفت انگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضی دانان بلکه دانشمندان بسیاری از رشته های دیگر را به خود جلب کرده.
رابطهٔ دنبالهٔ فیبوناچی به این شکل است:
برای مثال برای به دست آوردن جملهٔ دهم باید جملهٔ نهم ( ۳۴ ) و جملهٔ هشتم ( ۲۱ ) را با هم جمع کنیم که برابر ۵۵ می شود.
چند فرمول برای احتساب جملهٔ n - اُم دنبالهٔ فیبوناچی، بدون استفاده از جمله های ماقبل وجود دارد.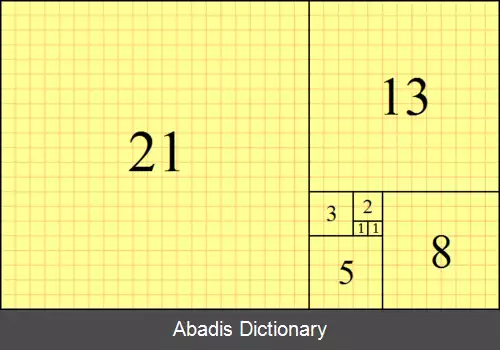



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفغیر از دو عدد اول، اعداد بعدی از جمعِ دو عددِ قبلیِ خود به دست می آیند. اولین اعداد این سری عبارت اند از:
این اعداد به نام لئوناردو فیبوناچی، ریاضی دان ایتالیاییِ قرن سیزدهم میلادی، نام گذاری شده است.
در واقع، فیبوناچی در سال ۱۲۰۲ به مسئله عجیبی علاقه مند شد. او می خواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آن ها تعریف کند در نهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود:
• شما یک جفت خرگوش نر و ماده دارید که همین الان به دنیا آمده اند.
• خرگوش ها پس از یک ماه بالغ می شوند.
• دوران بارداری خرگوش ها یک ماه است.
• هنگامی که خرگوش ماده به سن بلوغ می رسد حتماً باردار می شود.
• در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده به دنیا می آورد.
• خرگوش ها هرگز نمی میرند.
حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت؟
فرض کنیم x n تعداد جفت خرگوش پس از n ماه باشد، می دانیم که x 1 = 1 , x 2 = 1 ، تعداد جفت خرگوشها در ماه n + 1 - اُم برابر خواهد بود با حاصل جمع تعداد جفت خرگوش هایی که در این ماه متولد می شوند با تعداد جفت خرگوشهای موجود ( x n ) . اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هم اکنون حداقل دو ماه سن خواهند داشت و به سن زادوولد رسیده اند. تعداد جفت خرگوش های متولد شده برابر خواهد بود با x n − 1 ، پس خواهیم داشت:
x۱ = ۱ , x۲ = ۱ , xn + ۱ = xn + xn - ۱
که اگر از قواعد مذکور پیروی کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است.
۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴, …
فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفت انگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضی دانان بلکه دانشمندان بسیاری از رشته های دیگر را به خود جلب کرده.
رابطهٔ دنبالهٔ فیبوناچی به این شکل است:
برای مثال برای به دست آوردن جملهٔ دهم باید جملهٔ نهم ( ۳۴ ) و جملهٔ هشتم ( ۲۱ ) را با هم جمع کنیم که برابر ۵۵ می شود.
چند فرمول برای احتساب جملهٔ n - اُم دنبالهٔ فیبوناچی، بدون استفاده از جمله های ماقبل وجود دارد.





wiki: اعداد فیبوناچی
