اصل هاردی - واینبرگ ( که به آن HWP، تعادل هاردی - واینبرگ، قضیه هاردی واینبرگ یا قانون هاردی - واینبرگ نیز گفته می شود ) به این صورت بیان می شود که فرکانس الل ها و ژنوتیپ در یک جمعیت از نسلی به نسل دیگر ثابت می ماند - یا در تعادل است - در صورتی که عوامل مختل کننده خاصی رخ ندهد. از جمله این عوامل مختل کننده می توان به جهش، انتخاب طبیعی، شارش ژن و جفت گیری غیرتصادفی اشاره کرد. نکته مهم این جاست که در یک جمعیت واقعی همواره یکی از این عوامل مختل کننده وجود خواهد داشت. در واقع تعادل هاردی - واینبرگ بیان کننده شرایط ایدئال است. فرکانس الل هایی که در یک جمعیت ثابت فرض می شوند عبارتند از: عدم جهش، عدم مهاجرت، جمعیت نامتناهی و عدم وجود فشار انتخاب طبیعی علیه هر کدام از ژنوتیپ ها. در ساده ترین حالت و با وجود ۲ فرض می کنیم الل غالب را با A و الل دیگر را با a و فرکانس آن ها را به ترتیب با p و q نمایش می دهیم. در صورتی که جفت گیری به صورت اتفاقی رخ دهد در این صورت حاصل جفت گیری دارای فرکانس F r e q ( A A ) = p 2 برای AA و دارای F r e q ( A a ) = 2 p q برای Aa و دارای F r e q ( a a ) = q 2 برای aa در جمعیت خواهد بود.
... [مشاهده متن کامل]
حالت بهتر - اما معادل – توصیف احتمالی برای HWP آن است که برای نسل بعدی و برای هر فردالل ها به صورت تصادفی و مستقل از یکدیگر انتخاب خواهند شد. دو الل a و A با فرکانس های به ترتیب q و p را در یک جمعیت در نظر بگیرید. راه های مختلف برای بدست آوردن ژنوتیپ ها با استفاده از شکل زیر بدست می آید:
این فرمول گاهی به صورت 2 ( p q ) + ( p ) 2 + ( q ) 2 = 1 نوشته می شود که بیانگر این حقیقت است که مجموع احتمالات باید برابر ۱ شود. سه ژنوتیپ های نهایی در انجام این زاد و ولد عبارتند از:
• f ( A A ) = p 2 {\displaystyle f ( \mathbf {AA} ) =p^{2}\, }
• f ( A a ) = 2 p q {\displaystyle f ( \mathbf {Aa} ) =2pq\, }
• f ( a a ) = q 2 {\displaystyle f ( \mathbf {aa} ) =q^{2}\, }
این فرکانس ها، فرکانس های هاردی - واینبرگ نامیده می شوند. این فرکانس ها در یک جمعیت و با فرض جفت گیری اتفاقی و اندازه جمعیت نامحدود به دست می آیند. گاهی اوقات یک جمعیت از کنار هم قرار دادن جنس مؤنث و جنس مذکر ایجاد می شود در این حالت فرض اول برای تعادل هاردی - واینبرگ برقرار نخواهد بود و جمعیت نسل اول در تعادل هاردی - واینبرگ قرار نخواهد داشت ولی نسل های بعدی در تعادل هاردی - واینبرگ قرار خواهند داشت.
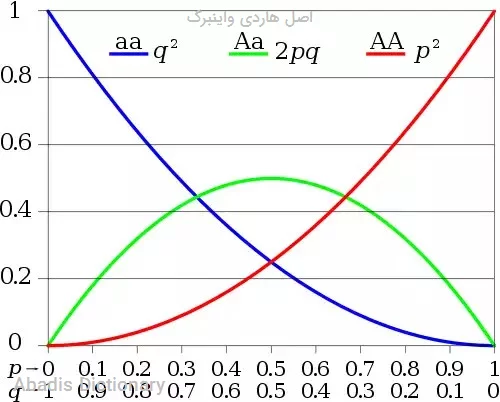
... [مشاهده متن کامل]
حالت بهتر - اما معادل – توصیف احتمالی برای HWP آن است که برای نسل بعدی و برای هر فردالل ها به صورت تصادفی و مستقل از یکدیگر انتخاب خواهند شد. دو الل a و A با فرکانس های به ترتیب q و p را در یک جمعیت در نظر بگیرید. راه های مختلف برای بدست آوردن ژنوتیپ ها با استفاده از شکل زیر بدست می آید:
این فرمول گاهی به صورت 2 ( p q ) + ( p ) 2 + ( q ) 2 = 1 نوشته می شود که بیانگر این حقیقت است که مجموع احتمالات باید برابر ۱ شود. سه ژنوتیپ های نهایی در انجام این زاد و ولد عبارتند از:
این فرکانس ها، فرکانس های هاردی - واینبرگ نامیده می شوند. این فرکانس ها در یک جمعیت و با فرض جفت گیری اتفاقی و اندازه جمعیت نامحدود به دست می آیند. گاهی اوقات یک جمعیت از کنار هم قرار دادن جنس مؤنث و جنس مذکر ایجاد می شود در این حالت فرض اول برای تعادل هاردی - واینبرگ برقرار نخواهد بود و جمعیت نسل اول در تعادل هاردی - واینبرگ قرار نخواهد داشت ولی نسل های بعدی در تعادل هاردی - واینبرگ قرار خواهند داشت.

