اسپلاین (ریاضیات). یک تکه بند[ نیازمند منبع] ( به انگلیسی: spline ) یا اسپلاین در ریاضیات تابع خاصی است که به صورت تکه ای ( چندضابطه ای ) توسط چندجمله ای ها تعریف می شود. [ ۱] در مسائل درون یابی، درون یابی تکه بندی از درون یابی جندجمله ای ارجحیت دارد، زیرا منجر به نتایج مشابه می شود، حتی اگر از چندجمله ای با درجه پایین استفاده کنیم، همچینین از پدیده رونگه برای درجه های بالاتر جلوگیری می کند.
اسپلاین ( spline ) در ریاضیات یک تابع هموار چندضابطه ای - چندجمله ای است.
در مسائل درون یابی، معمولاً منظور از درون یابی اسپلاین، پیدا کردن چندجمله ای درون یابی است، چرا که به همان نتیجه می انجامد، حتی در مواقعی که از چندجمله ای های درجه پایین استفاده می شود. چندجمله ای های پارا متری از درجات بالا یک ضعف دارند: برای مثال در شکل زیر پرش ارتفاع در حوالی مرکز داده ها باعث تغییر زیادی روی چندجمله ای درون یابی شده در نزدیکی انتهای منحنی دارد.
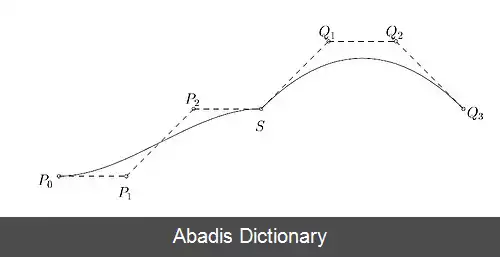
در عوض در شکل بعدی از منحنی اسپلاین درجه سوم ( cubic spline ) در همان نقاط مثال قبل استفاده شده است. مشاهده می کنید که منحنی چقدر دقیق از نقاط ورودی می گذرد. دقت داشته باشید که همواره منحنی ها در محل اتصال شکلی یکنواخت دارند.
منحنی اسپیلاین با استفاده از مشتقات یک منحنی چندجمله ای درجه سوم میان هر دو نقطه ورودی ایجاد می شود. به عبارتی دیگر، منحنی درجه سوم و تابع چندضابطه ای است که از چند تابع چند ضابطه ای که به یکدیگر چسبیده اند تشکیل شده است. این توابع چند ضابطه ای آن چنان در محل اتصال با یکدیگر مطابقت دارند که تقریباً محل اتصال مشخص نیست. در حقیقت، اگر تمام تابع با یک تابع p ( t ) توصیف شود، p ( t ) آن قدر یکنواخت و هموار خواهد بود که دارای مشتق دوم در تمام نقاط و مشتق دوم پیوسته خواهد بود.
اسپلاین درجه سوم یک منحنی چند ضابطه ای درجه سوم با مشتق دوم پیوسته است.
کلمهٔ اسپلاین در حقیقت بازمی گردد به نوار باریکی از جنس چوب یا فلز. در گذشته منحنی ها برای طراحی کشتی ها و هواپیماها با قرار دادن دقیق منحنی هایی از نوارهای باریک چوب یا فلز در بدنهٔ آن ها به گونه ای که ضمن گذشتن از نقاط دلخواه انعطاف پذیر نیز باشند. به دلایل فیزیکی، این چنین منحنی هایی تقریباً چند ضابطه ای هایی درجه سوم با مشتق دوم پیوسته اند، در صورتی که به درستی پارامتری شوند.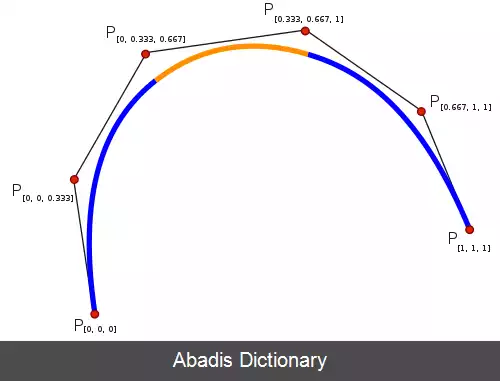



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاسپلاین ( spline ) در ریاضیات یک تابع هموار چندضابطه ای - چندجمله ای است.
در مسائل درون یابی، معمولاً منظور از درون یابی اسپلاین، پیدا کردن چندجمله ای درون یابی است، چرا که به همان نتیجه می انجامد، حتی در مواقعی که از چندجمله ای های درجه پایین استفاده می شود. چندجمله ای های پارا متری از درجات بالا یک ضعف دارند: برای مثال در شکل زیر پرش ارتفاع در حوالی مرکز داده ها باعث تغییر زیادی روی چندجمله ای درون یابی شده در نزدیکی انتهای منحنی دارد.
در عوض در شکل بعدی از منحنی اسپلاین درجه سوم ( cubic spline ) در همان نقاط مثال قبل استفاده شده است. مشاهده می کنید که منحنی چقدر دقیق از نقاط ورودی می گذرد. دقت داشته باشید که همواره منحنی ها در محل اتصال شکلی یکنواخت دارند.
منحنی اسپیلاین با استفاده از مشتقات یک منحنی چندجمله ای درجه سوم میان هر دو نقطه ورودی ایجاد می شود. به عبارتی دیگر، منحنی درجه سوم و تابع چندضابطه ای است که از چند تابع چند ضابطه ای که به یکدیگر چسبیده اند تشکیل شده است. این توابع چند ضابطه ای آن چنان در محل اتصال با یکدیگر مطابقت دارند که تقریباً محل اتصال مشخص نیست. در حقیقت، اگر تمام تابع با یک تابع p ( t ) توصیف شود، p ( t ) آن قدر یکنواخت و هموار خواهد بود که دارای مشتق دوم در تمام نقاط و مشتق دوم پیوسته خواهد بود.
اسپلاین درجه سوم یک منحنی چند ضابطه ای درجه سوم با مشتق دوم پیوسته است.
کلمهٔ اسپلاین در حقیقت بازمی گردد به نوار باریکی از جنس چوب یا فلز. در گذشته منحنی ها برای طراحی کشتی ها و هواپیماها با قرار دادن دقیق منحنی هایی از نوارهای باریک چوب یا فلز در بدنهٔ آن ها به گونه ای که ضمن گذشتن از نقاط دلخواه انعطاف پذیر نیز باشند. به دلایل فیزیکی، این چنین منحنی هایی تقریباً چند ضابطه ای هایی درجه سوم با مشتق دوم پیوسته اند، در صورتی که به درستی پارامتری شوند.





wiki: اسپلاین (ریاضیات)
