استنتاج معکوس روند استنتاج رو به عقب در مسائل و موقعیت ها با مراحل محدود، جهت به دست آوردن اقدام بهینه در هر مرحله است. در ریاضیات این نوع استنتاج یکی از اصلی ترین راه حل های حل مسائل پویا از جمله معادله بلمن می باشد. در نظریه بازی ها نیز از استنتاج معکوس برای پیدا کردن تعادل نش زیربازی کامل استفاده می کنند که در بازی های پویا کاربرد دارد. [ ۱]
استنتاج معکوس اولین بار توسط بنیان گذاران نظریه بازی ها، جان فون نیومن و اسکار مورگنشترن در سال ۱۹۹۶ به کار برده شد. [ ۲]
نام های دیگری که برای این استنتاج در زبان فارسی استفاده می شود، استقرای معکوس یا استقرای عقب گرد می باشد.
روند استنتاج معکوس به صورت تجزیه و تحلیل یک بازی از آخرین مرحله به ابتدای آن است و در هر مرحله استراتژی که مغلوب است، حذف می شود و استراتژی برنده در گام بعدی بازی تحلیل می شود. در واقع در هر مرحله فرض می شود، هر بازیکن با انتخاب عقلانی استراتژی که سود بیشتری دارد را انتخاب می کند. برای مثال شکل فرم گسترده بازی دونفره زیر را در نظر بگیرید:
بازی از سه مرحله تشکیل شده و در مرحله اول، بازیکن اول بین دو استراتژی X و W باید یکی را انتخاب کند، در مرحله دوم بازیکن دوم با انتخاب در دو راس ۲ و ۳ مواجه است که در راس دوم دو استراتژی C و D و در راس سوم دو استراتژی A , B را دارد. در صورتی که بازیکن اول در مرحله اول W و بازیکن دوم در مرحله دوم C را انتخاب کند، بازیکن اول در مرحله سوم حق انتخاب بین دو استراتژی Y و Z را دارد. سود هر بازیکن در رأس های نهایی درخت ذکر شده است که اولین عدد ( عدد سمت راست ) سود بازیکن اول و دومین عدد، سود نفر دوم است.
برای به دست آوردن تعادل نش زیربازی کامل در این بازی، که تعادلی است که هر بازیکن بهترین پاسخ را در هر مرحله به اقدام حریف انجام می دهد، از این استنتاج به این صورت استفاده می کنیم که از آخرین راس ( راس با ارتفاع بیشتر از ریشه ) شروع می کنیم. بازیکن اول در این مرحله با انتخاب استراتژی Y، سود ۴ و با دیگری ۱ را می برد. پس با انتخاب عقلانی، استراتژی اول را انتخاب می کند و استراتژی Z مغلوب این استراتژی است. پس بازی به شکل زیر کاهش پیدا می کند.
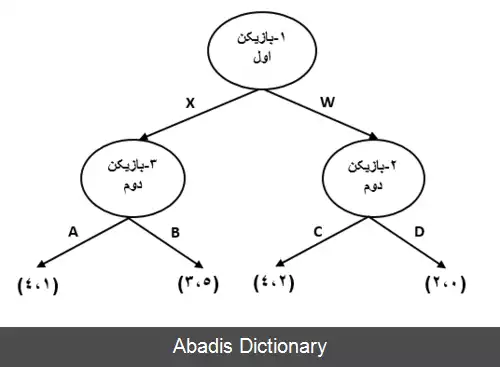
در نتیجه استراتژی پروفایل ( ۴٬۲ ) به استراتژی های نفر دوم در راس ۳ اضافه می شود. در مرحله دوم، بازیکن دوم در دو راس باید تصمیم گیرد، در راس دوم، بیشترین سود این بازیکن انتخاب B است و در راس اول C. پس دو استراتژی دیگر متناظرا مغلوب این دو استراتژی می شوند. پس شکل کاهش یافته سوم به دست می آید.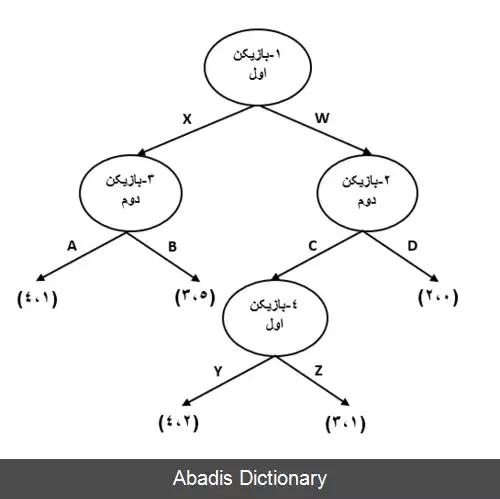
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاستنتاج معکوس اولین بار توسط بنیان گذاران نظریه بازی ها، جان فون نیومن و اسکار مورگنشترن در سال ۱۹۹۶ به کار برده شد. [ ۲]
نام های دیگری که برای این استنتاج در زبان فارسی استفاده می شود، استقرای معکوس یا استقرای عقب گرد می باشد.
روند استنتاج معکوس به صورت تجزیه و تحلیل یک بازی از آخرین مرحله به ابتدای آن است و در هر مرحله استراتژی که مغلوب است، حذف می شود و استراتژی برنده در گام بعدی بازی تحلیل می شود. در واقع در هر مرحله فرض می شود، هر بازیکن با انتخاب عقلانی استراتژی که سود بیشتری دارد را انتخاب می کند. برای مثال شکل فرم گسترده بازی دونفره زیر را در نظر بگیرید:
بازی از سه مرحله تشکیل شده و در مرحله اول، بازیکن اول بین دو استراتژی X و W باید یکی را انتخاب کند، در مرحله دوم بازیکن دوم با انتخاب در دو راس ۲ و ۳ مواجه است که در راس دوم دو استراتژی C و D و در راس سوم دو استراتژی A , B را دارد. در صورتی که بازیکن اول در مرحله اول W و بازیکن دوم در مرحله دوم C را انتخاب کند، بازیکن اول در مرحله سوم حق انتخاب بین دو استراتژی Y و Z را دارد. سود هر بازیکن در رأس های نهایی درخت ذکر شده است که اولین عدد ( عدد سمت راست ) سود بازیکن اول و دومین عدد، سود نفر دوم است.
برای به دست آوردن تعادل نش زیربازی کامل در این بازی، که تعادلی است که هر بازیکن بهترین پاسخ را در هر مرحله به اقدام حریف انجام می دهد، از این استنتاج به این صورت استفاده می کنیم که از آخرین راس ( راس با ارتفاع بیشتر از ریشه ) شروع می کنیم. بازیکن اول در این مرحله با انتخاب استراتژی Y، سود ۴ و با دیگری ۱ را می برد. پس با انتخاب عقلانی، استراتژی اول را انتخاب می کند و استراتژی Z مغلوب این استراتژی است. پس بازی به شکل زیر کاهش پیدا می کند.
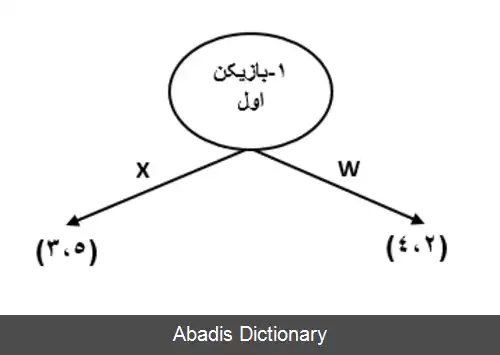
در نتیجه استراتژی پروفایل ( ۴٬۲ ) به استراتژی های نفر دوم در راس ۳ اضافه می شود. در مرحله دوم، بازیکن دوم در دو راس باید تصمیم گیرد، در راس دوم، بیشترین سود این بازیکن انتخاب B است و در راس اول C. پس دو استراتژی دیگر متناظرا مغلوب این دو استراتژی می شوند. پس شکل کاهش یافته سوم به دست می آید.




wiki: استنتاج معکوس
