آزمون خطای استاندارد میانگین. آزمون Z نوعی آزمون آماری است که توزیع آماره ی آزمون تحت فرضیه ی صفر می تواند به صورت یک توزیع نرمال تخمین زده شود. به علت قضیه حد مرکزی بیشتر آماره های آزمون برای تعداد زیاد نمونه، به صورت تقریبی با توزیع نرمال قابل تخمین زدن هستند. برای هر سطحی معنادار بودن آزمون Z یک مقدار بحرانی دارد ( برای مثال ۱/۹۶ برای ۵٪ دو طرفه ) که نسبت به آزمون t راحتی بیشتری ایجاد می کند زیرا در آزمون t برای هر تعداد نمونه یک مقدار بحرانی مشخص وجود دارد. برای همین در بیشتر آزمون های آماری در صورتی که واریانس جمعیت مشخص باشد یا تعداد نمونه ها زیاد باشد به راحتی می توان به صورت تقریبی از آزمون Z استفاده کرد. در صورتی که واریانس جمعیت مشخص نباشد ( و لازم باشد که از روی نمونه ها به دست آورده شود ) یا تعداد نمونه ها کم باشد ( کم تر از ۳۰ ) ، آزمون t مناسب تر از این آزمون است.
اگر T یک آماره باشد که تحت فرض صفر به صورت تقریبی از توزیع نرمال پیروی کند، قدم بعدی برای انجام دادن آزمون Z محاسبه ی امید ریاضی T است. فرض کنید مقدار آن θ باشد. در این صورت اگر انحراف معیار T را نیز حساب کنیم و آن را s بنامیم، عدد Z به دست آمده برابر Z = ( T − θ ) s خواهد بود که با استفاده از این عدد می توانیم پی - مقدار یک طرفه یا دوطرفه را حساب کنیم. این مقدار برای آزمون یک طرفه برابر Φ ( Z ) برای سمت راست یا Φ ( − Z ) برای سمت چپ است. در آزمون دوطرفه نیز این مقدار برابر 2 Φ ( | Z | ) است که Φ همان تابع استاندارد توزیع تجمعی نرمال است.
برای اینکه آزمون Z قابل اعمال روی داده ها باشد باید در شرایطی صدق کنند:
• پارامترهای Nuisance باید مشخص باشد یا با دقت بالایی تخمین زده شود ( یکی از مثال های این پارامتر انحراف معیار است ) . آزمون Z فقط روی یک پارامتر تمرکز دارد و تمام پارامترهای نامشخص را به صورت ثابت در مقدار واقعی آن ها فرض می کند.
• آماره ی آزمون باید از توزیع نرمال پیروی کند. بعضی ها ممکن است با قضیه حد مرکزی توجیه کنند که آماره ی آزمون از توزیع نرمال پیروی می کند. تحقیق های بسیاری در این زمینه انجام شده است که در چه مواقعی آماره ی آزمون به صورت تقریبی از توزیع نرمال پیروی می کند. اگر این آماره به صورت قوی از نرمال پیروی نکند، آزمون Z نباید استفاده شود.
فرض کنید که در یک منطقه ی جغرافیایی میانگین و انحراف معیار نمرات یک امتحان به ترتیب ۱۰۰ نمره و ۱۲ نمره باشد. می خواهیم نمرات ۵۵ دانش آموز را در مدرسه ای بررسی کنیم. میانگین نمرات این دانش آموزان ۹۶ است. حال سؤال این است که آیا میانگین این دانش آموزان به صورت معنا داری پایین تر از دانش آموزان منطقه است یا خیر. یا به عبارتی دیگر آیا میانگین نمرات این دانش آموزان به صورت شگفت انگیزی پایین تر از دانش آموزان منطقه است یا خیر.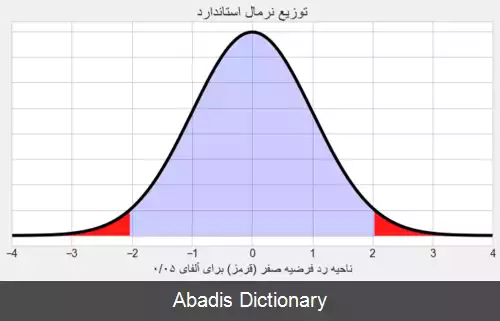
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر T یک آماره باشد که تحت فرض صفر به صورت تقریبی از توزیع نرمال پیروی کند، قدم بعدی برای انجام دادن آزمون Z محاسبه ی امید ریاضی T است. فرض کنید مقدار آن θ باشد. در این صورت اگر انحراف معیار T را نیز حساب کنیم و آن را s بنامیم، عدد Z به دست آمده برابر Z = ( T − θ ) s خواهد بود که با استفاده از این عدد می توانیم پی - مقدار یک طرفه یا دوطرفه را حساب کنیم. این مقدار برای آزمون یک طرفه برابر Φ ( Z ) برای سمت راست یا Φ ( − Z ) برای سمت چپ است. در آزمون دوطرفه نیز این مقدار برابر 2 Φ ( | Z | ) است که Φ همان تابع استاندارد توزیع تجمعی نرمال است.
برای اینکه آزمون Z قابل اعمال روی داده ها باشد باید در شرایطی صدق کنند:
• پارامترهای Nuisance باید مشخص باشد یا با دقت بالایی تخمین زده شود ( یکی از مثال های این پارامتر انحراف معیار است ) . آزمون Z فقط روی یک پارامتر تمرکز دارد و تمام پارامترهای نامشخص را به صورت ثابت در مقدار واقعی آن ها فرض می کند.
• آماره ی آزمون باید از توزیع نرمال پیروی کند. بعضی ها ممکن است با قضیه حد مرکزی توجیه کنند که آماره ی آزمون از توزیع نرمال پیروی می کند. تحقیق های بسیاری در این زمینه انجام شده است که در چه مواقعی آماره ی آزمون به صورت تقریبی از توزیع نرمال پیروی می کند. اگر این آماره به صورت قوی از نرمال پیروی نکند، آزمون Z نباید استفاده شود.
فرض کنید که در یک منطقه ی جغرافیایی میانگین و انحراف معیار نمرات یک امتحان به ترتیب ۱۰۰ نمره و ۱۲ نمره باشد. می خواهیم نمرات ۵۵ دانش آموز را در مدرسه ای بررسی کنیم. میانگین نمرات این دانش آموزان ۹۶ است. حال سؤال این است که آیا میانگین این دانش آموزان به صورت معنا داری پایین تر از دانش آموزان منطقه است یا خیر. یا به عبارتی دیگر آیا میانگین نمرات این دانش آموزان به صورت شگفت انگیزی پایین تر از دانش آموزان منطقه است یا خیر.

