اریبی یک برآوردگر. در آمار، تابع اریبی، [ ۱] تورِش یا بایاس ( به انگلیسی: bias ) یک برآوردگر، همان اختلاف بین امید ریاضی آن برآوردگر و مقدار واقعی پارامتر تخمین زده شده می باشد. برآوردگر یا قانون تصمیم گیری با اریبی صفر را نااریب[ ۲] یا بدون تورش می گویند. در غیر این صورت، به برآوردگر اریب یا تورش دار نامیده می شود.
اریبی عبارتی معنادار دربارهٔ یک تابع می باشد، و در حالی که ویژگی مطلوب نیست، نمی توان آن را تنزل داد. به عبارت ریاضی، فرض کنید داده x i , i = 1 , … , n بر اساس توزیع P ( x | θ ) توزیع شده باشند و θ ^ یک تخمین گر براساس داده های مشاهده باشد. اریبی θ ^ به صورت زیر تعریف می شود:
که در آن E امید ریاضی متغیر x نسبت به توزیع P ( x | θ ) است.
می توان با توجه به میانه نیز اریبی را اندازه گیری کرد، ولی با میانگین نه، در شرایطی که یکی میانه نااریب را از میانگین نااریب معمول جدا می کند. اریبی به برآوردگر سازگار مربوط می شود که در آن، برآوردگرهای استوار، همگرا و به طور مجانبی، نااریب اند ( از این رو به مقداری صحیح همگرا اند ) ، اگرچه برآوردگرهای مفرد در یک دنباله استوار، ممکن است اریب باشند ( به طوری که اریبی به صفر همگرا باشد ) .
یک برآوردگر نااریب به یک برآوردگر اریب ترجیح داده می شود، اما در عمل، بقیه برابر نیستند، و اغلب از برآوردگرهای اریبی با اریبی های کوچک استفاده می شود. زمانی که از برآوردگر اریبی استفاده می گردد، اریبی نیز تخمین زده می شود. یک برآوردگر اریبی می تواند به دلایل مختلفی به کار رود: زیرا یک برآوردگر نااریب، بدون فرض های بعدی دربارهٔ یک جامعه وجود نخواهد داشت، یا محاسبه آن دشوار خواهد بود؛ زیرا یک برآوردگر میانه - نااریب می باشد، ولی میانگین - نااریب نیست ( یا برعکس ) ؛ زیرا یک برآوردگر اریب بخشی از تابع از دست رفته را در مقایسه با برآوردگر نااریب کاهش می دهد ( به ویژه خطای مربع میانگین ) ؛ یا زیرا در برخی شرایط نااریب بودن تحت برخی تحولات محافظت نمی شود، برخی میانه - نااریبی محافظت می شود؛ مثلاً واریانس نمونه یک برآوردگر نااریب برای واریانس جامعه است، اما جذر آن، انحراف معیار استاندارد، یک برآوردگر اریب برای انحراف معیار جامعه استاندارد است.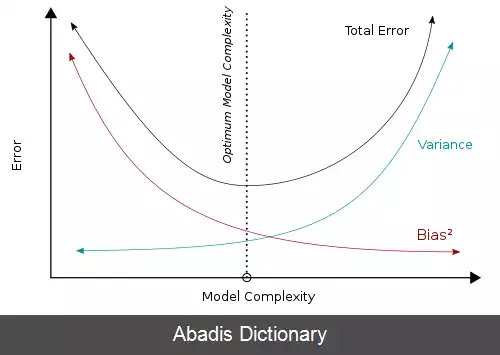
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاریبی عبارتی معنادار دربارهٔ یک تابع می باشد، و در حالی که ویژگی مطلوب نیست، نمی توان آن را تنزل داد. به عبارت ریاضی، فرض کنید داده x i , i = 1 , … , n بر اساس توزیع P ( x | θ ) توزیع شده باشند و θ ^ یک تخمین گر براساس داده های مشاهده باشد. اریبی θ ^ به صورت زیر تعریف می شود:
که در آن E امید ریاضی متغیر x نسبت به توزیع P ( x | θ ) است.
می توان با توجه به میانه نیز اریبی را اندازه گیری کرد، ولی با میانگین نه، در شرایطی که یکی میانه نااریب را از میانگین نااریب معمول جدا می کند. اریبی به برآوردگر سازگار مربوط می شود که در آن، برآوردگرهای استوار، همگرا و به طور مجانبی، نااریب اند ( از این رو به مقداری صحیح همگرا اند ) ، اگرچه برآوردگرهای مفرد در یک دنباله استوار، ممکن است اریب باشند ( به طوری که اریبی به صفر همگرا باشد ) .
یک برآوردگر نااریب به یک برآوردگر اریب ترجیح داده می شود، اما در عمل، بقیه برابر نیستند، و اغلب از برآوردگرهای اریبی با اریبی های کوچک استفاده می شود. زمانی که از برآوردگر اریبی استفاده می گردد، اریبی نیز تخمین زده می شود. یک برآوردگر اریبی می تواند به دلایل مختلفی به کار رود: زیرا یک برآوردگر نااریب، بدون فرض های بعدی دربارهٔ یک جامعه وجود نخواهد داشت، یا محاسبه آن دشوار خواهد بود؛ زیرا یک برآوردگر میانه - نااریب می باشد، ولی میانگین - نااریب نیست ( یا برعکس ) ؛ زیرا یک برآوردگر اریب بخشی از تابع از دست رفته را در مقایسه با برآوردگر نااریب کاهش می دهد ( به ویژه خطای مربع میانگین ) ؛ یا زیرا در برخی شرایط نااریب بودن تحت برخی تحولات محافظت نمی شود، برخی میانه - نااریبی محافظت می شود؛ مثلاً واریانس نمونه یک برآوردگر نااریب برای واریانس جامعه است، اما جذر آن، انحراف معیار استاندارد، یک برآوردگر اریب برای انحراف معیار جامعه استاندارد است.

wiki: اریبی یک برآوردگر
